Durbin-Watson檢定統計量臨界值表

發表於 | 分類於
字數統計 1779
影響Durbin-Watson檢定統計量的因素很多，一一給予數值後，即可透過機率分配模擬器得到對應之抽樣分配，找到臨界值

1. 介紹

「自我相關」一直是研究時間序列數據或序列相關數據的專家學者們非常想知道的數值。偏偏這個問題始終無法解決。李玫郁從2013年開始投稿Durbin-Watson檢定統計量相關研究至各大期刊區，極少數願意接受這類的論文。原因在於李玫郁認為Durbin and Watson兩人的檢定公式有問題，起因於他們並未發覺Durbin-Watson檢定統計量受到如此多因素的影響，而使用檢定公式的灰色地帶。所謂灰色地帶是指Durbin-Watson檢定的檢定公式，使用 $d_{L}$ 和 $d_{U}$ 判斷是否拒絕虛無假設1, 2, 3。

這種作法和統計分析的點估計量抽樣分配得到之臨界值觀念產生矛盾。正常的作法如同我們常用的標準常態分配、t分配、卡方分配等，臨界值和累積機率是一對一且映成，不會有灰色地帶發生。

為什麼Durbin-Watson檢定統計量的臨界值怎麼會有上下界呢？很簡單的可以回答這個問題：太多因素影響Durbin-Watson檢定統計量之抽樣分配，導致他們找不出Durbin-Watson檢定統計量之抽樣分配。

2. 錯誤：大樣本下的Durbin-Watson test臨界值仍有灰色地帶

有意思的是即使到很大的樣本個數依舊存在上下界(參考下圖 4, 5 )。

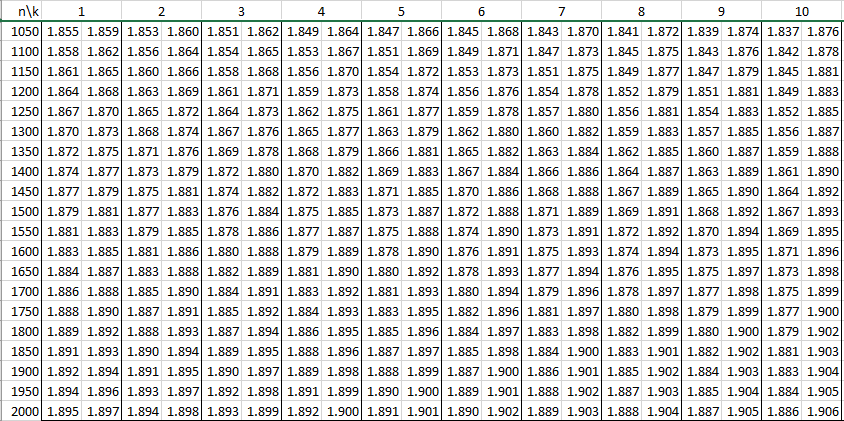
如果真的知道多少樣本可以讓Durbin-Watson檢定統計量之抽樣分配趨近常態分配，那麼又怎麼會有如上圖或Turner(2019)的大樣本的Durbiin-Watson檢定之臨界值一文呢！

3. 2013年Durbin-Watson檢定統計量抽樣分配已經開始被研究

李玫郁從2013年到2016年皆有Durbin-Watson檢定統計量的期刊論文6, 7，到2022年在美國亞馬遜網路書店出版【Demythologize Durbin-Watson Test Statistic】，正式為Durbin-Watson檢定統計量確定抽樣分配，以及說明影響因素如何改變抽樣分配。因為找出了抽樣分配，臨界值和累積機率存在一對一且映成關係，不會發生灰色地帶問題，正式改善Durbin-Watson檢定公式和臨界值表。

3.1. 如何找抽樣分配

想要知道Durbin-Watson檢定統計量抽樣分配就得從檢定統計量的設計開始下手，特別是Durbin-Watson檢定統計量是由迴歸的殘差組成之數學組合，所以會影響殘差的因素都要被考量進入。

影響因素

在傳統線性迴歸下，線性迴歸模型成為期望值模型的函數形式，自變數和應變數都應被視為隨機變數，其數值服從特定分配。因此，將有哪些因素會影響Durbin-Watson檢定統計量抽樣分配呢？

  • 自變數
  • 自我相關係數
  • lag期數
  • 一階自我相關誤差模型的誤差分配($u_{t}$)
  • 截距估計值
  • 斜率估計值
  • 誤差分配的變異數

根據文獻，Durbin-Watson檢定統計量架構在

  • 自變數不影響檢定統計量
  • 落後一期
  • 只討論是否有自我相關(自我相關係數為0或非0)，(詳情參考註腳9內容)
  • 誤差分配為期望值=0的常態分配
  • 沒討論過截距、斜率、變異數是否影響檢定統計量

機率分配模擬器就可用在這

機率分配模擬器是找出Durbin-Watson檢定統計量抽樣分配的重要工具。機率分配模擬器可以模擬出自變數和一階自我相關誤差模型的誤差分配，然後設定好自我相關係數值、落後期數值、一次的樣本數、截距、斜率、變異數後，根據Durbin-Watson檢定統計量公式，生成出一個各地Durbin-Watson值。那要生成多少Durbin-Watson值才能代表抽樣分配？答案是1億筆！(詳情參考註腳9內容)

3.2. Durbin-Watson檢定擁有正確臨界值表的優勢

  • 檢定公式完全符合一般的點估計量特性

    ：由機率分配模擬器得到的Durbin-Watson檢定統計量臨界值不再有灰色地帶。

  • 自我相關係數可以檢定任何介於-1到1的數值

    ：現階段的Durbin-Watson檢定只能檢定有無自我相關係數，不管自我相關係數會是其他值。但正常的檢定是可以檢定任何值的。由機率分配模擬器得到不同自我相關係數下的Durbin-Watson臨界值就能夠檢定介於-1和1之間的任何值。

  • 可檢定不同落後期下的自我相關

    ：原本的Durbin-Watson檢定受限臨界值表，只能在落後1期的設定下做自我相關檢定。當機率分配模擬器驗證過可找出不同落後期的Durbin-Watson檢定統計量之抽樣分配後，自然可用於不同的落後期數下的自我相關檢定。

小結

Durbin-Watson檢定的灰色地帶是該檢定的最大問題，卻從Durbin and Watson到現在都還被使用。這樣的檢定統計量沒有問題，發生問題的原因是抽樣分配找不到。從2013年開始，Durbin-Watson檢定統計量的抽樣分配已經可以被機率分配模擬器找出來，代表影響Durbin-Watson檢定統計量的抽樣分配的因素已然確定。

長達8年的時間，Durbin-Watson在研究和應用上始終沒有改變，甚至大樣本該趨近常態分配的臨界值(2016年期刊論文已經發表，參考註腳7和9)，卻仍產生有上下界的臨界值結果(參考註腳4~6)。這已然說明Durbin-Watson臨界值計算的近似法有問題！

Durbin-Watson檢定用於Recurrent Neural Network(RNN)也只能檢定是否存在自我相關(或序列相關)而已。若說RNN有多準確，恐怕從一開始的序列相關確認就產生問題了。當然引入正確的Durbin-Watson檢定後，不只沒有檢定公式的灰色地帶，還可以確認出正確的自我相關係數，讓RNN的資料集和訓練資料集皆可更具備正確的數據特性，誤差也可以更小。

參考資料

  1. real-statistics介紹 Durbin-Watson test ↩

  2. Wiki百科介紹 Durbin-Watson檢定統計量 ↩

  3. CFI認證機構的Durbin-Watson test介紹 ↩

  4. real-statistics介紹 Durbin-Watson表 ↩

  5. 樣本數到2000的 Durbin-Watson表 ↩

  6. 期刊論文：Mei-Yu Lee, 2016, On the Durbin-Watson Statistic Based on a Z-Test in Large Samples, International Journal of Computational Economics and Econometrics, 6(1), 114-121. ↩

  7. 公開論文：Mei-Yu Lee on SSRN ↩