二維常態分配介紹

發表於 | 分類於
字數統計 1524

1. 前言

一組數據可以檢測出來服從特定機率分配，通常稱為「邊際機率分配」。兩組數據除可各自找出服從何種分配外，還可以找聯合機率分配(Joint probability distribution)。

所謂聯合機率分配是對應聯合機率和兩隨機變數形成一定關係。你可以想像這是一個函數關係，

  • 應變數 = 聯合機率
  • 自變數 = 隨機變數1、隨機變數2

在統計學中最常使用的就是常態分配，並且如果多個隨機變數，也希望能夠是獨立隨機取得。在這樣的假設下，統計學如果有兩獨立的隨機變數，並且其邊際機率分配為常態分配，則聯合機率分配稱為二維常態分配。

2. 二維常態分配

二維常態分配的特性就在於兩隨機變數獨立，使得兩隨機變數的關係為「圓」，亦是立體空間投影在底面積的形狀。

假設有兩獨立隨機變數，$X_{1}, X{_2}$，服從常態分配，$N(\mu, \sigma^{2}$。

  • 聯合機率密度函數
\[f_{X_{1},X_{2}}(x_{1},x_{2})=\frac{1}{2 \,\pi \, \sigma_{x_{1}} \, \sigma_{X_2} \, \sqrt{1-\rho^{2}}} \times e^{-\frac{Q}{2(1-\rho^{2})}}\]

其中，$Q$為

\[Q = Z_{X_{1}}^{2} - 2 \rho \, Z_{X_{1}} \, Z_{X_{2}} + Z_{X_{2}}^{2}\]

其中，$\rho$ 為相關係數，$Z_{X_{1}}$ 為隨機變數$X_{1}$標準化，$Z_{X_{2}}$ 為隨機變數 $X_{2}$ 標準化。

2.1. 點估計

  • 期望值
    • $E(X_{1})=\overline{X}_{1}$
    • $E(X_{2})=\overline{X}_{2}$
  • 變異數
    • $Var(X_{1})=S_{X_{1}}^{2}=\frac{\sum_{i=1}^{n} \left(X_{1,i}-\overline{X}_{1} \right)^{2}}{n-1}$
    • $Var(X_{2})=S_{X_{2}}^{2}=\frac{\sum_{i=1}^{n} \left(X_{2,i}-\overline{X}_{2} \right)^{2}}{n-1}$
  • 相關係數
    • $r=\frac{\sum_{i=1}^{n} \varepsilon_{X_{1}} \, \varepsilon_{X_{2}}}{\sqrt{\sum_{i=1}^{n} \varepsilon_{X_{1}}^{2} \, \sqrt{\sum_{i=1}^{n} \varepsilon_{X_{2}}^{2}}}}$

2.2. 當 $\rho = 0$，聯合機率密度函數為

\[f_{X_{1},X_{2}}(x_{1},x_{2})=\frac{1}{2 \,\pi \, \sigma_{x_{1}} \, \sigma_{X_2}} \times e^{-\frac{Z_{X_{1}}^{2}+Z_{X_{2}}^{2}}{2}}\]

2.3. 條件機率分配

在 $X_{2}$為條件下，$X_{1}$的條件機率分配為常態分配，即

\[X_{1} \vert X_{2} \sim N \left(\mu_{X_{1}}+\frac{\rho \, \sigma_{X_1}}{\sigma_{X_{2}}} \, (X_{2}-\mu_{X_{2}}), \,(1-\rho^{2}) \, \sigma_{X_{1}}^{2} \right)\]

2.3.1. 從線性概念來看

\[\begin{matrix} \mu_{X_{1}}+\frac{\rho \, \sigma_{X_1}}{\sigma_{X_{2}}} \, (X_{2}-\mu_{X_{2}}) \\ = \alpha_{0}+\alpha_{1} \, X_{2} \\ = E(X_{1} \vert X_{2}) \end{matrix}\]

對照係數可得到

\[\mu_{X_{1}} - \alpha_{1} \mu_{X_{2}} = \alpha_{0}\]

$\alpha_{0}$ 為截距，代表$X_{2}$ 對 $E(X_{1} \vert X_{2})$ 的固定影響，和

\[\frac{\rho \, \sigma_{X_1}}{\sigma_{X_{2}}} \, = \alpha_{1}\]

$\alpha_{1}$ 為斜率，代表$X_{2}$ 對 $E(X_{1} \vert X_{2})$ 的邊際影響。

2.3.2. 相關係數和斜率關係

  • 正相關係數 $\Longleftrightarrow$ 正斜率
  • 負相關係數 $\Longleftrightarrow$ 負斜率
  • 相關係數 = 0 $\Longleftrightarrow$ 斜率 = 0

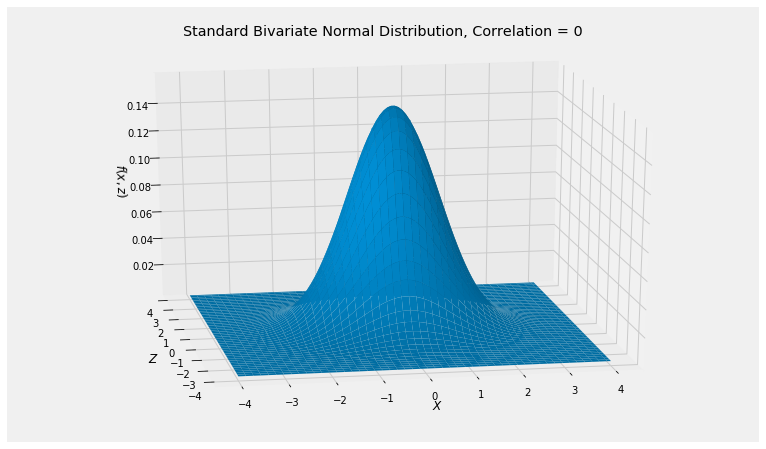
3. 圖形

  • 來自R軟體1

  • IPython 2

  • ScienceDirect 3

  • Excel

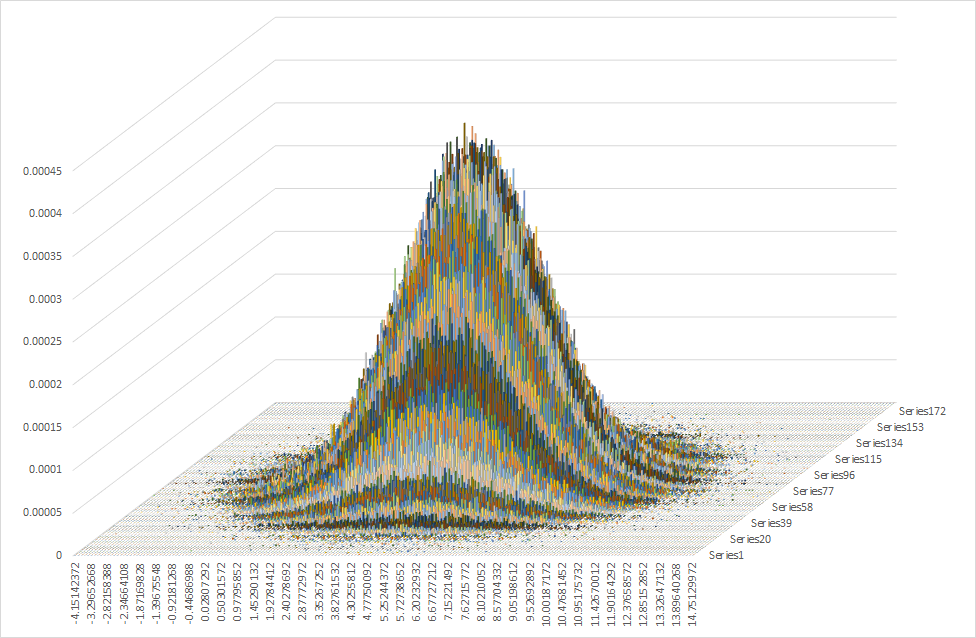
  • prob140.org 4

3.1. 如何使用Excel繪製

對辦公室行政人員最常接觸的軟體就是 MicroSoft Office。他們想學數據分析的最低入手成本即使用Excel。

那麼如何運用Excel畫出二維常態分配的立體圖？

  • 第一步：生成兩獨立隨機變數，各隨機變數的隨機樣本來自常態分配，$N(\mu = 5, \sigma=2)$。
  • 第二步：建立每個成對樣本的數對，計算相對次數。
  • 第三步：匯入Excel。欄為 $X_{1}$ 的隨機樣本值，列為 $X_{2}$ 的隨機樣本值。欄列形成的交叉儲存格填入相對次數值。此處須使用「sumproduct」函數對應到交叉的儲存格中。
  • 第四步：選擇相對次數的所有儲存格，點擊【插入】⇨【圖表】⇨直方圖⇨立體直方圖。然後等待圖形出現。
  • 第五步：編輯數據，同列不同欄的數字成為橫軸。

4. 小結

二維常態分配是迴歸分析和多變量分析的基礎。若隨機變數獨立服從常態分配，則底面積為標準的圓形，然而，若有有線性相關，則底面積則會呈現橢圓形，甚至趨近線性。

至於繪製二維常態分配的方法有很多。最簡單的方式是使用機率密度函數，數學模擬繪製。然而這樣的做法缺少了隨機性，我們便可使用機率分配模擬器，同時生成隨機樣本數對和相對次數。此時，即可畫出二維常態分配的3D立體圖。

這類的隨機樣本3D立體圖還可適用於多個隨機變數。我們將隨機變數分為兩類。兩類的隨機變數依據自己需要，做數學計算，成為新的變數。所以兩類的隨機變數群轉換成兩隨機變數，符合3D立體圖的底面積兩軸。而我們又可再次繪製3D立體圖。

參考資料

  1. Google論壇：請問如何畫出二元常態分配的立體圖形 ↩

  2. 艾鍗學院：高斯模糊 ↩

  3. ScienceDirect：Bivarate Normal distribution，內容的圖4-7。 ↩

  4. hprob140.org 的 Bivariate Normal Distribution ↩