1. 預測股價方法
- 使用的自變數
- 時間序
- 前一日開盤價
- 前一日最高價
- 前一日最低價
- 前一日收盤價
- 使用的應變數
- 當日收盤價
- 三種模型組合後成為數據的數學模型方程式
- 建立期望值數學模型:從基本8種的基本數學模式中挑選出最小MSE的模型
- 建立MAD變異數異質性模型:從基本10種的基本數學模型中挑選出最小MSE的模型。此模型可產生應變數的上下波動
- 加入一階自我相關誤差迴歸模型
- 運算預測值的區間估計
- 運算在近N日為條件下,預測明日上漲的條件機率和下跌的條件機率
2. 數據
- 數據來源:台灣證券交易所
- 數據類型:日資料
- 數據期間:從當日數據往前推500筆(相當二年又一季的數據)
2. 預測結果
2.1. 台股指數於2022/04/15預測結果
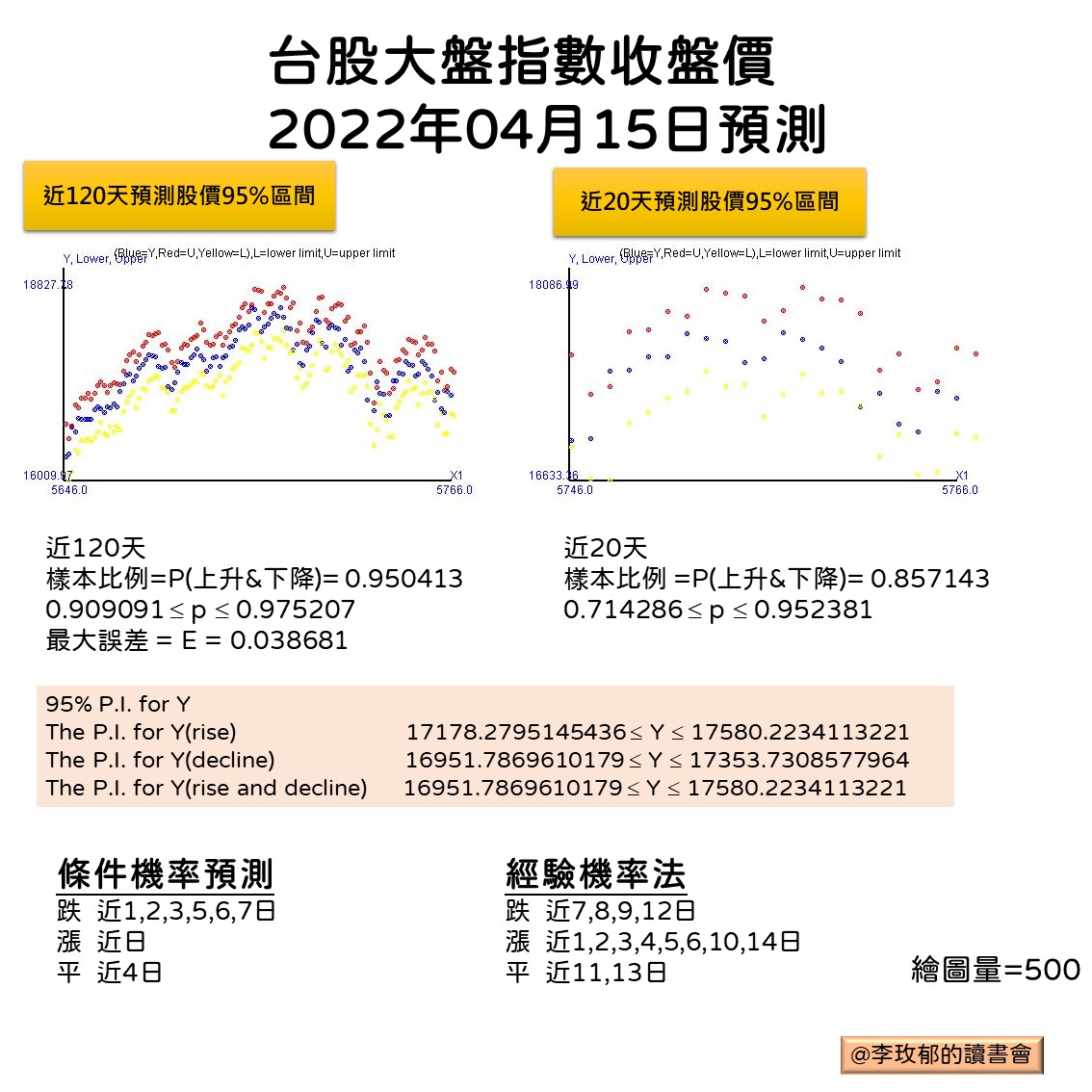
2.1.1. 近120天
- 樣本比例=P(上升&下降)= 0.950413
- $0.909091 \leq p \leq 0.975207$
- 最大誤差 = E = 0.038681
2.1.2. 近20天
- 樣本比例 =P(上升&下降)= 0.857143
- $0.714286 \leq p \leq 0.952381$
2.1.3. 點估計預測值= 17262.47
2.1.4. 95%預測區間
The P.I. for Y(rise)
\[17178.2795145436 \leq Y \leq 17580.2234113221\]The P.I. for Y(decline)
\[16951.7869610179 \leq Y \leq 17353.7308577964\]The P.I. for Y(rise and decline)
\[16951.7869610179 \leq Y \leq 17580.2234113221\]2.1.5. 條件機率預測
| 近N日為條件 | 條件機率漲跌 |
|---|---|
| 1,2,3,5,6 | 跌 |
| 無 | 漲 |
| 4 | 平 |
3.1.6. 經驗機率法
| 近N日為條件 | 條件機率漲跌 |
|---|---|
| 7,8,9,12 | 跌 |
| 1,2,3,4,5,6,10,14 | 漲 |
| 11,13 | 平 |
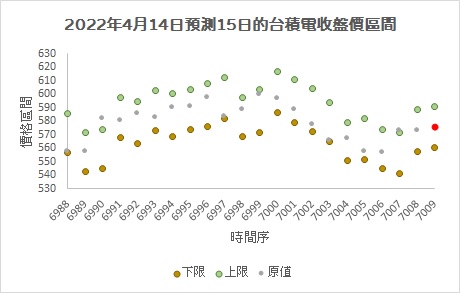
2.2. 台積電於2022/04/15預測結果
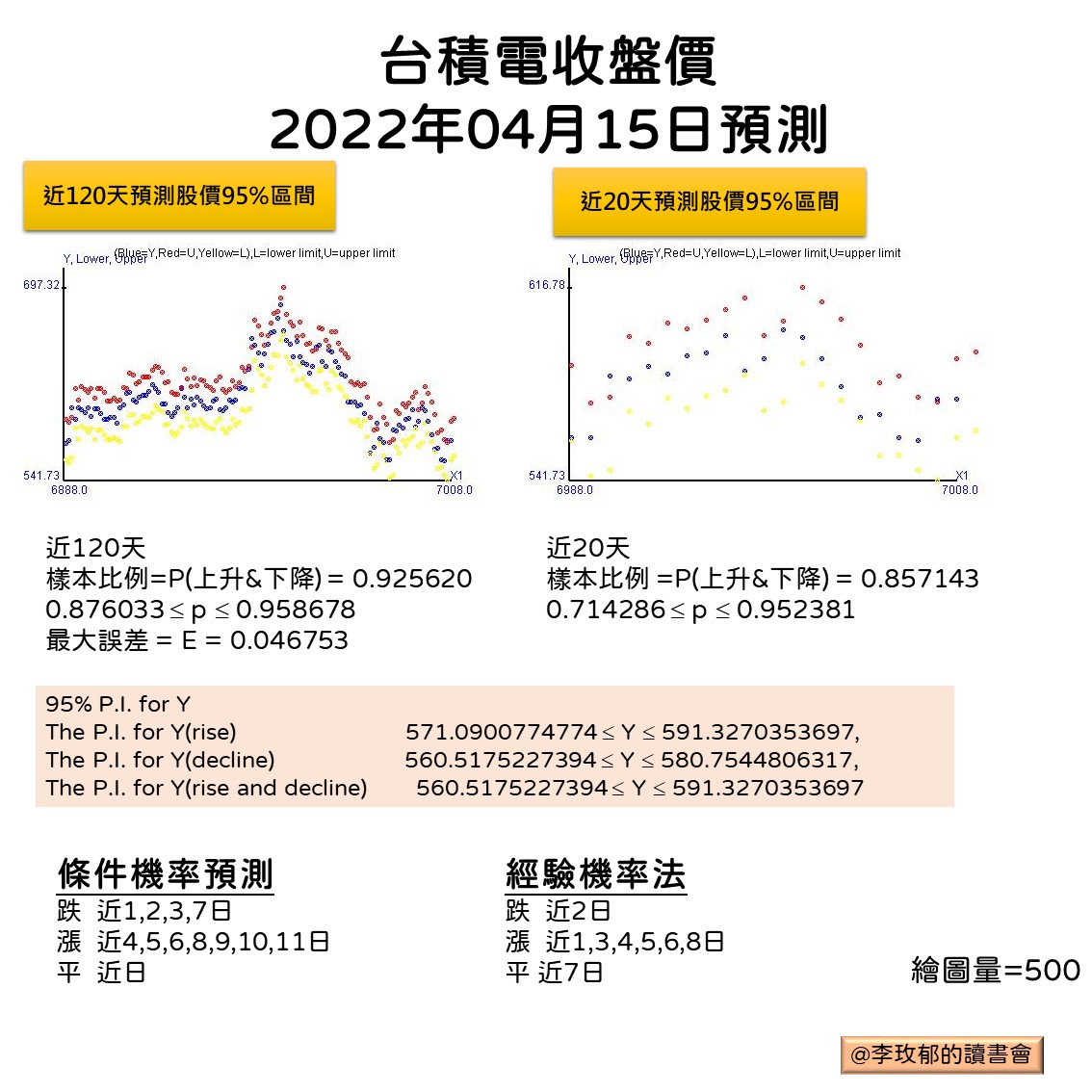
2.2.1. 近120天
- 樣本比例=P(上升&下降)= 0.925620
- $0.876033 \leq p \leq 0.958678$
- 最大誤差 = E = 0.046753
2.2.2. 近20天
- 樣本比例 =P(上升&下降)= 0.857143
- $0.7614286 \leq p \leq 0.952381$
2.2.3. 點估計預測值= 576.06
2.2.4. 95%預測區間
The P.I. for Y(rise)
The P.I. for Y(rise)
\[571.0900774774 \leq Y \leq 591.3270353697\]The P.I. for Y(decline)
\[560.5175227394 \leq Y \leq 580.7544806317\]The P.I. for Y(rise and decline)
\[560.5175227394 \leq Y \leq 591.3270353697\]2.2.5. 條件機率預測
| 近N日為條件 | 條件機率漲跌 |
|---|---|
| 1,2,3,7 | 跌 |
| 4,5,6,8,9,10,11 | 漲 |
| 無 | 平 |
3.3.6. 經驗機率法
| 近N日為條件 | 條件機率漲跌 |
|---|---|
| 2 | 跌 |
| 1,3,4,5,6,8 | 漲 |
| 7 | 平 |
3. 補充
有人詢問為什麼那些預測區間圖都沒有預測值。因為程式限制,加上一個預測點最終只會是成功或失敗,所以在預測區間圖上沒有顯示給大家看。
這種程式跑出來的結果,可保留原始運算結果,因此,我就用Excel讓大家理解,我們是可以將預測值加入預測區間內的。