1. 預測股價方法
- 使用的自變數
- 時間序
- 前一日開盤價
- 前一日最高價
- 前一日最低價
- 前一日收盤價
- 使用的應變數
- 當日收盤價
- 三種模型組合後成為數據的數學模型方程式
- 建立期望值數學模型:從基本8種的基本數學模式中挑選出最小MSE的模型
- 建立MAD變異數異質性模型:從基本10種的基本數學模型中挑選出最小MSE的模型。此模型可產生應變數的上下波動
- 加入一階自我相關誤差迴歸模型
- 運算預測值的區間估計
- 運算在近N日為條件下,預測明日上漲的條件機率和下跌的條件機率
2. 數據
- 數據來源:台灣證券交易所
- 數據類型:日資料
- 數據期間:從當日數據往前推500筆(相當二年又一季的數據)
2. 預測結果
2.1. 台股指數於2022/05/04預測結果
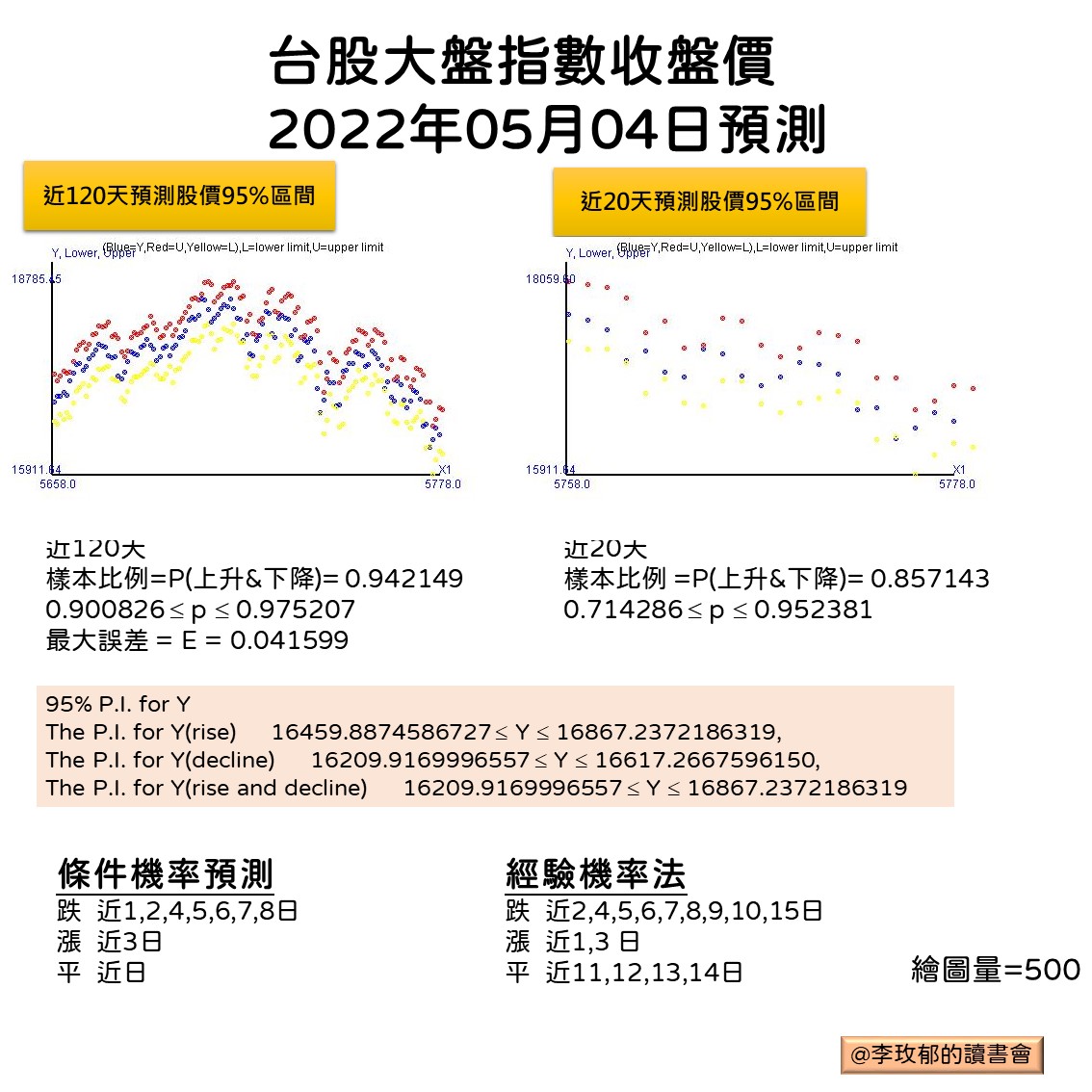
2.1.1. 近120天
- 樣本比例=P(上升&下降)= 0.942149
- $0.900826 \leq p \leq 0.975207$
- 最大誤差 = E = 0.041599
2.1.2. 近20天
- 樣本比例 =P(上升&下降)= 0.857143
- $0.714286 \leq p \leq 0.952381$
2.1.3. 點估計預測值= 16535.47
2.1.4. 95%預測區間
The P.I. for Y(rise) \(16459.8874586727 \leq Y \leq 16867.2372186319\) The P.I. for Y(decline) \(16209.9169996557 \leq Y \leq 16617.2667596150\) The P.I. for Y(rise and decline) \(16209.9169996557 \leq Y \leq 16867.2372186319\)
2.1.5. 條件機率預測
| 近N日為條件 | 條件機率漲跌 |
|---|---|
| 1,2,4,5,6,7,8 | 跌 |
| 3 | 漲 |
| 無 | 平 |
3.1.6. 經驗機率法
| 近N日為條件 | 條件機率漲跌 |
|---|---|
| 2,4,5,6,7,8,9,10,15 | 跌 |
| 1,3 | 漲 |
| 11,12,13,14 | 平 |
2.2. 台積電於2022/05/04預測結果
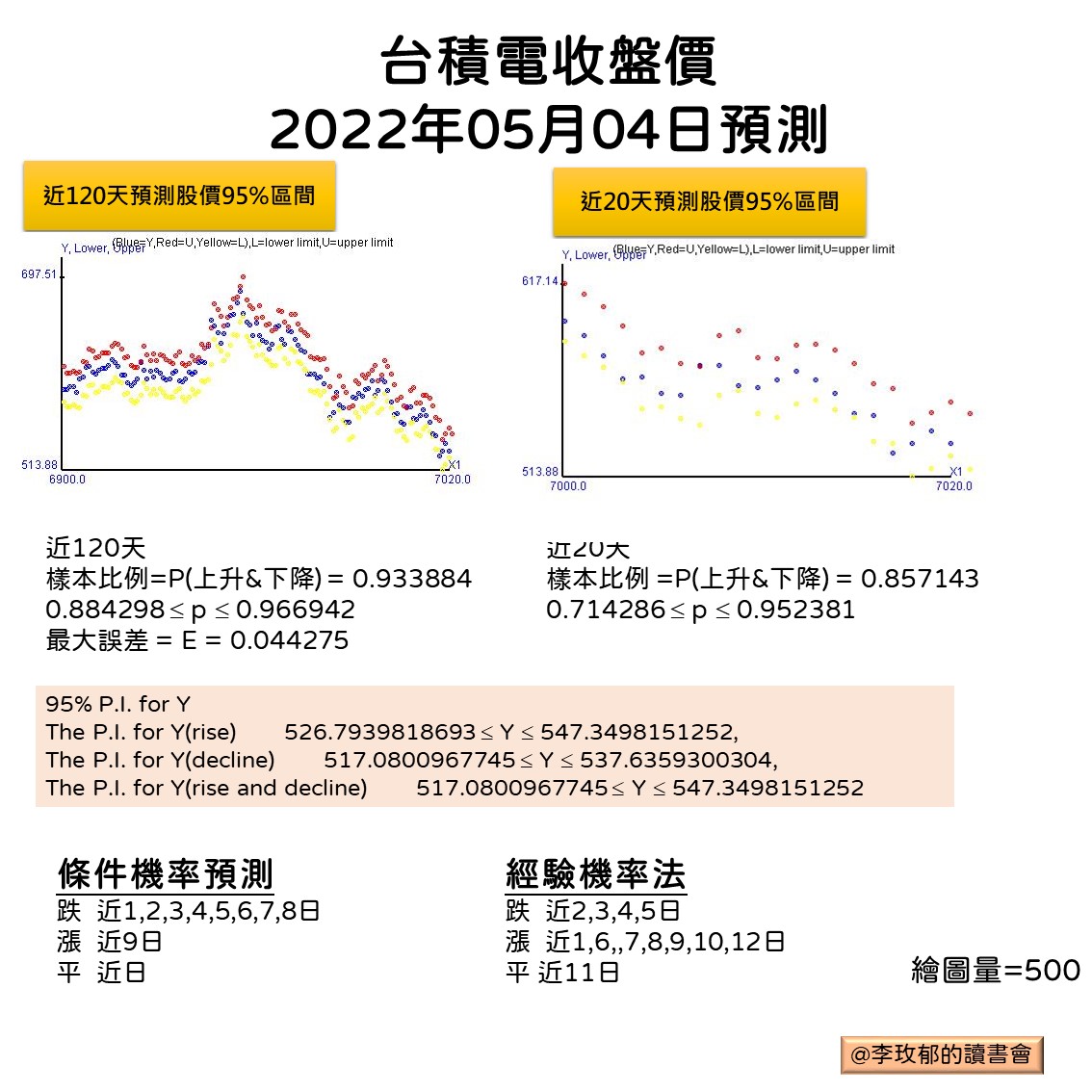
2.2.1. 近120天
- 樣本比例=P(上升&下降)= 0.933884
- $0.884298 \leq p \leq 0.966942$
- 最大誤差 = E = 0.044275
2.2.2. 近20天
- 樣本比例 =P(上升&下降)= 0.857143
- $0.7142865 \leq p \leq 0.952381$
2.2.3. 點估計預測值= 532.14
2.2.4. 95%預測區間
The P.I. for Y(rise) \(526.7939818693 \leq Y \leq 547.3498151252\) The P.I. for Y(decline) \(517.0800967745 \leq Y \leq 537.6359300304\) The P.I. for Y(rise and decline) \(517.0800967745 \leq Y \leq 547.3498151252\)
2.2.5. 條件機率預測
| 近N日為條件 | 條件機率漲跌 |
|---|---|
| 1,2,3,4,5,6,7,8 | 跌 |
| 9 | 漲 |
| 無 | 平 |
3.3.6. 經驗機率法
| 近N日為條件 | 條件機率漲跌 |
|---|---|
| 2,3,4,5 | 跌 |
| 1,6,7,8,9,10,12 | 漲 |
| 11 | 平 |