1. 前言
今天讓我分享機器學習的貝氏分類器觀念吧。我先圖解重點在下方。
不知道名詞定義,不知道使用限制,你以為的預測和專家學者說的預測是一樣的
貝氏分類器就是貝氏定理應用到機器學習中的產物。有沒有使用限制?當然有,可惜很多人並不理會,也未曾從基礎理解,認為機率可用於預測。因為他們所說的預測和常用的預測意思是不同的。
網路上很多在講貝氏分類器的文章,更有一篇網文想要告訴大家因為那些知名學校的學者在論文中使用了馬可夫鏈蒙地卡羅模擬法,或是分解機模型( factorization machine)就認為這樣機率做預測是正確的。
首先,你得先定義你的「預測」是指什麼。我們一般認知的預測是找出未來的未知值,稱為預測。這裡牽扯到時間問題。但是在談論機器學習所使用的「預測」是這種預測嗎?不是的。既然要用到機率,那機率最大的限制就是不存在「未知值」,它是在已知的事件「集合」定義出機率。如果你的事件不在集合內,使用這個機率就無效。
這些知名學者有沒有用錯機率觀念?沒有!因為他們認定的「預測」值還在事件集合內。你仍在這個集合內做事情,不適用「未知」事件上。
機率的定義已經限制你使用的範圍。
所謂的「預測」是在機率定義的集合內找出符合原始數據的數值,稱為預測值。
事件集合外的預測不能再用這個機率。你得重新改變事件集合,再計算出新的機率。
當你看到這些文章時,看起來很專業,實際上他們隱藏了你不知道的限制,讓你覺得這些方法很高大上。
2. 貝氏定理
2.1. 機率定義
機率是統計學的基礎,可稱為統計之母。你知道數據的機率模型,還需要統計分析嗎?當然,不需要!因為統計分析就是基於母體參數未知,尋找母體參數的科學方法。
那麼就讓我說說機率吧。詳細的機率介紹可參考臉書粉專-「高中數學與程式」。
機率的定義來自集合論。所謂樣本空間是宇集合確定後,特定一個事件就屬於各元素子集合的集合(=各事件子集合的集合)。機率就是特定事件發生所有可能的代表。使用符號表示為:
\[P(A)=\frac{n(A)}{n(\Omega = S)}\]上式中的$A$代表A事件,$n(\bullet)$代表某事件或集合的個數。$P(A)$代表A事件佔蒐集的所有可能狀況的比重。
注意到我寫的「蒐集到所有可能狀況」,這限制了你無法拿機率去預測未知。你只能預測「蒐集到所有可能狀況」會出現哪個。
開放性資料和時間序資料無法使用機率進行預測。
2.2. 機率種類
在說明機率前,我先定義
- 一組數據:一個欄位對應一個變數,該欄位記錄下的數據稱為一組數據
- 多組數據:會使用到多個欄位,每個欄位對應一個變數,並且每個欄位都記錄數據。
我們常用到的機率種類有三種:邊際機率、聯合機率、條件機率(含貝氏機率。
- 邊際機率來自特定組的數據就能計算其邊際機率。
- 聯合機率則是超過一組數據且數據個數相等,各組數據視為集合,其交集機率即為聯合機率。下圖為兩組數據解釋聯合機率。

- 條件機率同樣超過一組數據,並且各組數據之間有前後次序關係。它基於在前的集合為主下,同時具備前後集合特性的佔比。
2.2.1. 容易瞭解的方法
讓我用最容易理解的2 × 2 表和樹狀圖來說明機率關係。現存在兩個事件A和B,我們可以得到2 × 2 表,如下表,其特性如下列點。
- 2 × 2 表中間四格為聯合機率
- 第4欄和第4列為邊際機率
- 最右下角為總和,機率為1 = P(A) + P(非A) = P(B) + P(非B) = P(A ∩ B)+ P(A ∩ 非B) + P(非A ∩ B) + P(非A ∩ 非B)
| A | 非A | B的邊際機率 | |
|---|---|---|---|
| B | P(A ∩ B) | P(非A ∩ B) | P(B) |
| 非B | P(A ∩ 非B) | P(非A ∩ 非B) | P(非B) |
| A的邊際機率 | P(A) | P(非A) | P(Ω) |
條件機率來自前後關係,現在我想知道在A條件下發生B事件的可能機率為何。從2 × 2 表中看第2欄。
此時全部的事件個數僅有A事件的個數,n(A),對應機率為$P(A)$。你得從前述「僅有A事件個數」中挑出具有B事件的個數 = n(A ∩ B),對應機率為$ P(A ∩ B)$。從個數換成機率即為在A事件為條件下發生B的條件機率,
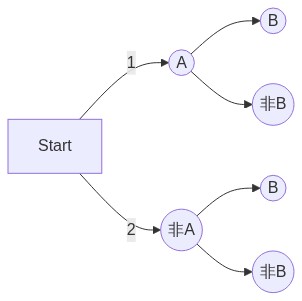
\[P(B|A)=\frac{n(A ∩ B)}{n(A)}\]第二種解釋方法是將2 × 2 表轉換為下方的樹狀圖。你會發現我們從【start】移到【A】點位置(已實現),條件機率指的就是A事件已經發生後,你已將站在【A】點,移動到【B】點的可能性。
上式還可以上下同除全部的個數,得到
\[P(B|A)=\frac{n(A ∩ B)/n(Ω)}{n(A)/n(Ω)}=\frac{P(A ∩ B)}{P(A)}\]那麼聯合機率可以由邊際機率和條件機率組成,
\[P(A ∩ B) = P(A) \times P(B|A)\]2.2.2. 常忽略聯合機率的計算
這只是來自A事件和B事件的兩組數據之機率值計算。通常難計算的是聯合機率。很多數據之間的聯合機率是難以被列完整的。所以我們可以用一組數據的邊際機率和迴歸分析得到的條件機率,根據上式得到聯合機率。
事實上,很多研究人員或演算法仍不管不問聯合機率的計算,即使他們認為這很重要,也需要計算出來,礙於做不到,且演算法也package好,就沒人知道聯合機率分配或將聯合機率分配視為理所當然存在,然後進行下一個步驟去了。
2.2.3. 貝氏定理
那貝氏定理呢?其實貝氏定理很容易理解,從2 × 2 表來看,只是從「欄」角度轉為「列」角度,重複條件機率的計算。你說難算嗎?你說難懂嗎?不難吧?!
那為什麼很多人覺得貝氏定理很難呢?因為他們在講的時候都用符號,讓人快暈倒,而且每個人在講的時候還用不同的中文或符號描述,搞得你昏頭轉向。但一個2 × 2 表就可以告訴你邊際、聯合、條件機率觀念,包含貝氏定理。
3. 小結
機器學習的貝氏分類器觀念非常簡單,用2 × 2 表就能讓所有人了解邊際、聯合、條件機率。而條件機率從欄列互轉就是條件轉貝氏。
講到事件的前後關係產生條件機率或貝氏機率,其實誰先誰後,你們真的知道嗎?多數都是由個人認定,就像我舉的例子,認為先A後B。不過當你取得數據後,你真的知道哪個欄位在前,哪個欄位在後嗎?是的!沒人知道,這都是人為認定的。
有人可能認為我可以測從A到B,再測從B到A,然後選最可能發生的結果。這合理嗎?當然不合理!
從條件機率可了解到條件機率的「條件」代表我們衡量的基準已經改變了。例如從【start】點已經移動到【A】點。你又如何去比較改變條件的兩個條件機率,而且用機率值高者決定從哪點移動到另一點呢?當我們使用基於貝氏定理的貝氏分類器時,數據欄位的前後關係已將被我們主觀認定了。
最後,機器學習的事前機率,也就是數據的邊際機率,是否來自數據正確的機率分配也是值得被懷疑的。這點可參考我其他的文章。如果沒有找出一組數據的機率分配,你又如何定出事前機率呢!
參考資料
[機器學習首部曲] 貝氏分類器 Bayesian Classifier
機器學習中的貝氏定理:生成模型 (Generative Model) 與判別模型 (Discriminative Model)