在前篇文章中介紹指數分配,這篇文章則是從指數分配和其他分配關係,進行模擬比對
1. 與均勻分配關係
假設兩獨立隨機變數,$X_{1}, X_{2}$,分別服從指數分配,參數為$\lambda$。
\[Y=\frac{X_{1}}{X_{1}+X_{2}} \sim U(0,1)\]
2. 與雙倍指數關係
假設兩獨立隨機變數,$X_{1}, X_{2}$,分別服從指數分配,參數為$\lambda$。
\[Y=X_{1}-X_{2} \sim Laplace(\lambda) \\ f_{Y}(y)=\frac{\lambda}{2} \, e^{-\lambda \vert y \vert}\]
3. 與柏拉圖分配關係
- 假設兩獨立隨機變數,$X_{1}, X_{2}$,分別服從指數分配,參數為$\lambda$。
此處的柏拉圖分配為型II,又稱為Lomax distribution。直接使用此分配的機率分配模擬器公式得到 Y2。
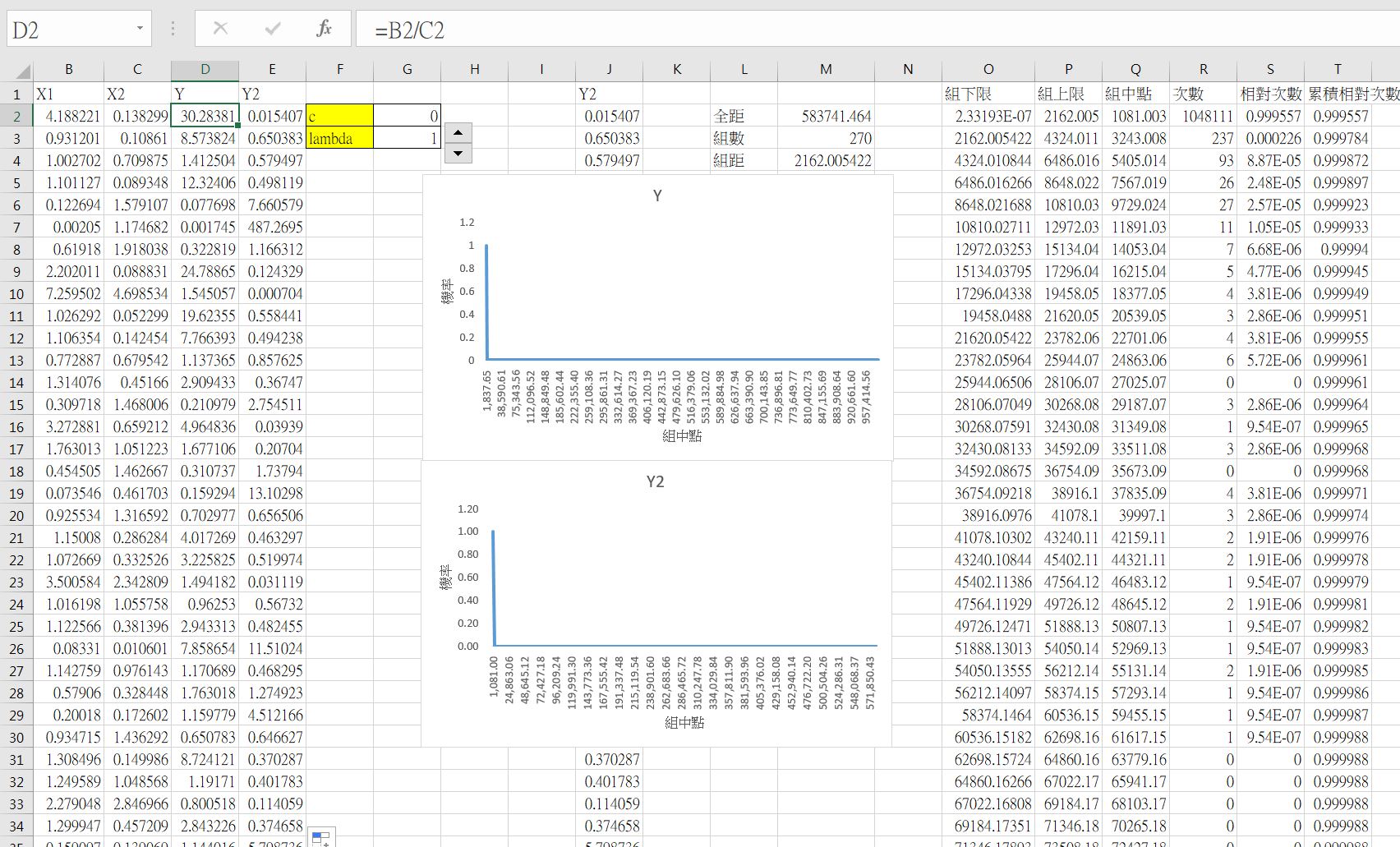
- 令$X$服從指數分配,參數為$\lambda$。
下圖中的 Y2 為直接使用柏拉圖1分配模擬數據。
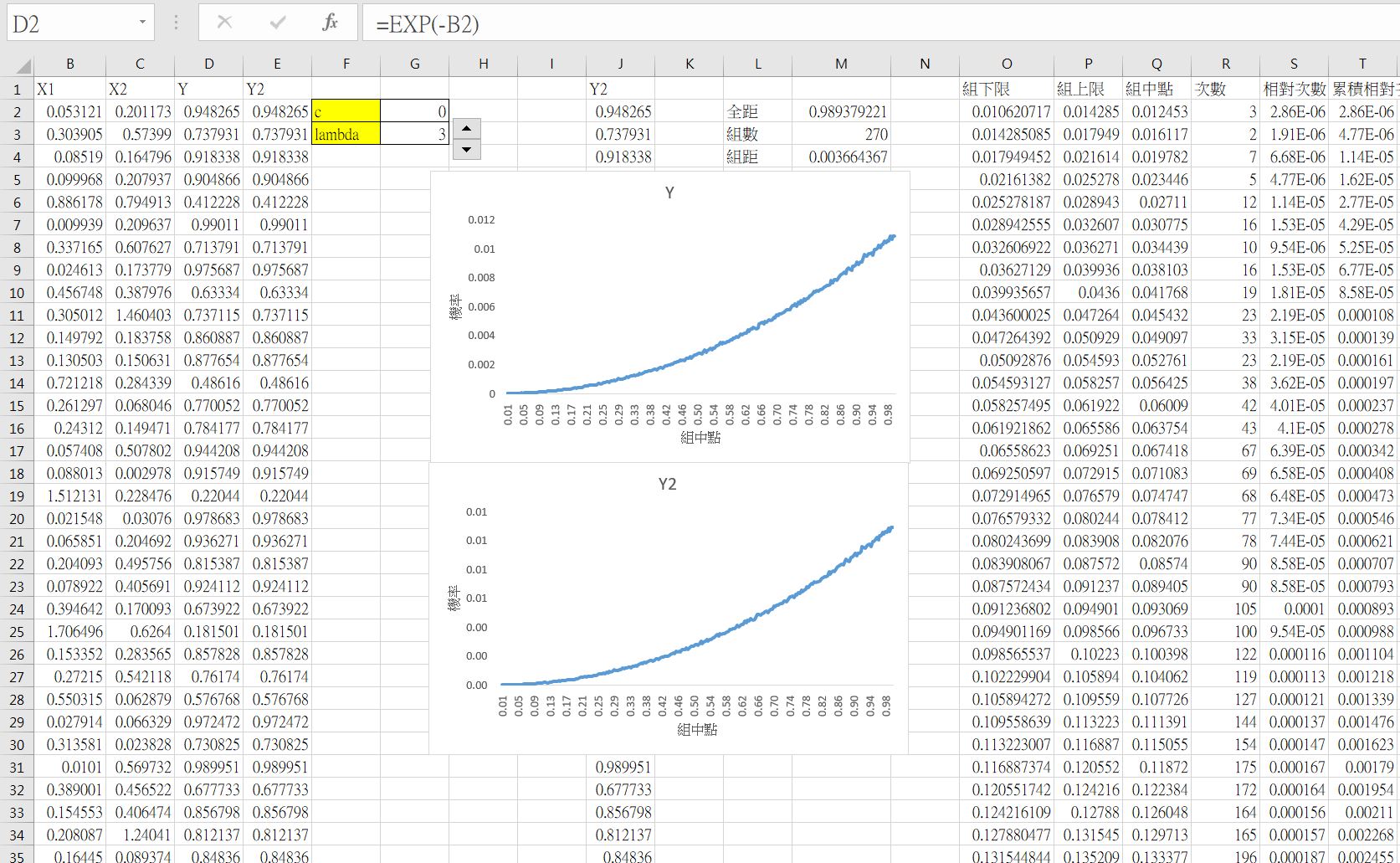
- 令$X$服從指數分配,參數為$\lambda$。
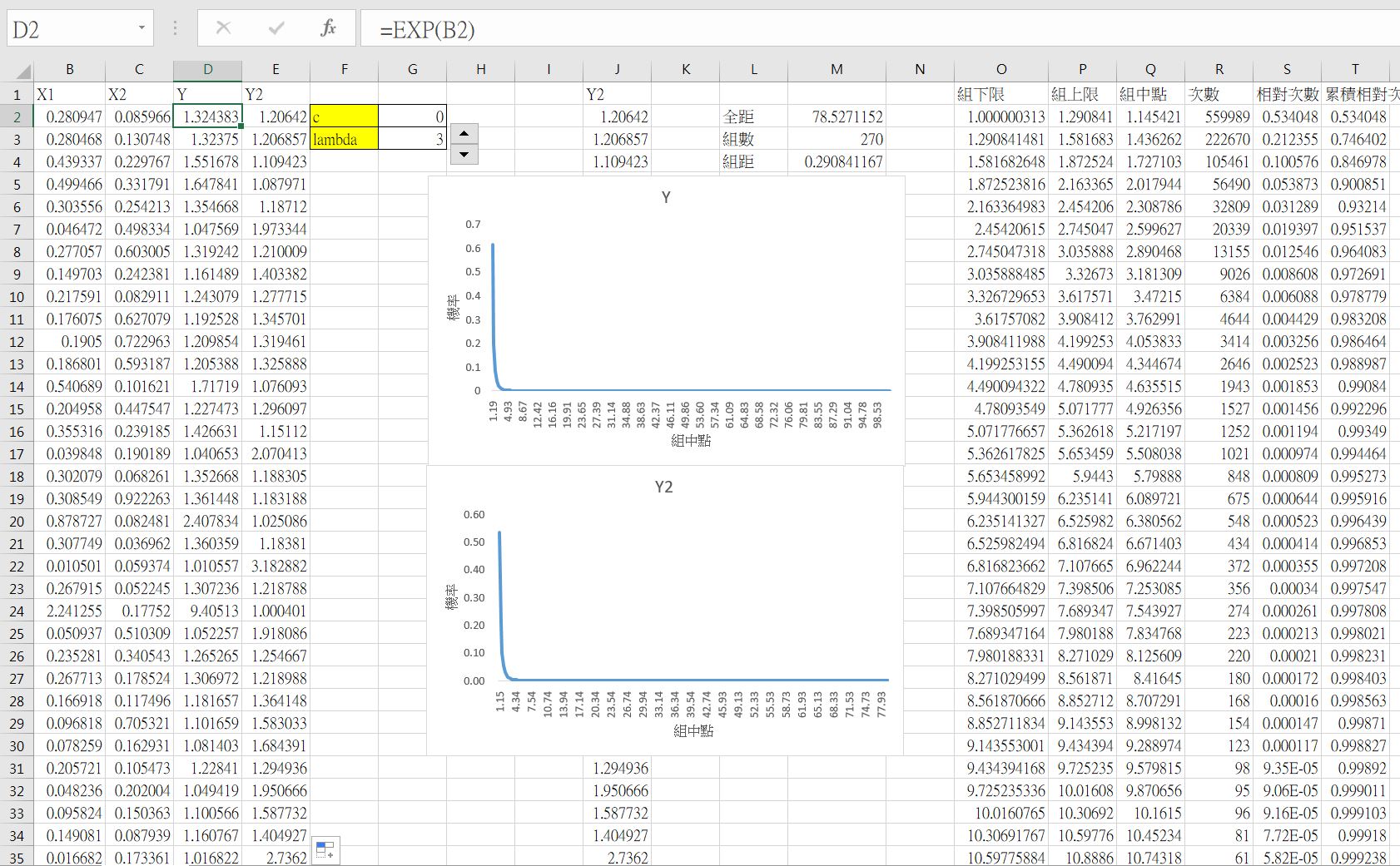
下圖中的 Y2 為直接使用柏拉圖3分配模擬數據。
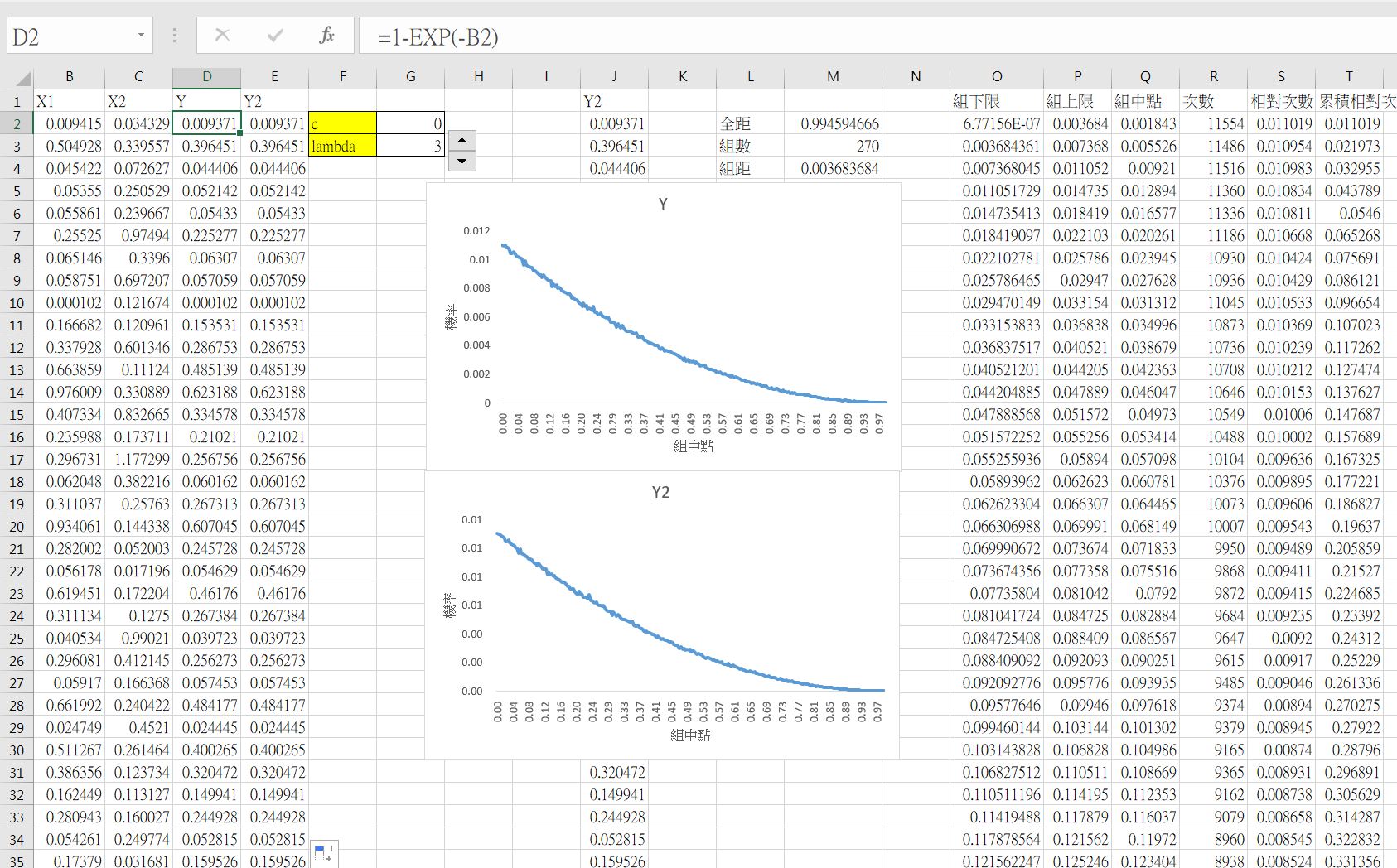
- 令$X$服從指數分配,參數為$\lambda$。
下圖中的 Y2 為直接使用柏拉圖2分配模擬數據。
4. 與雷利夫分配關係
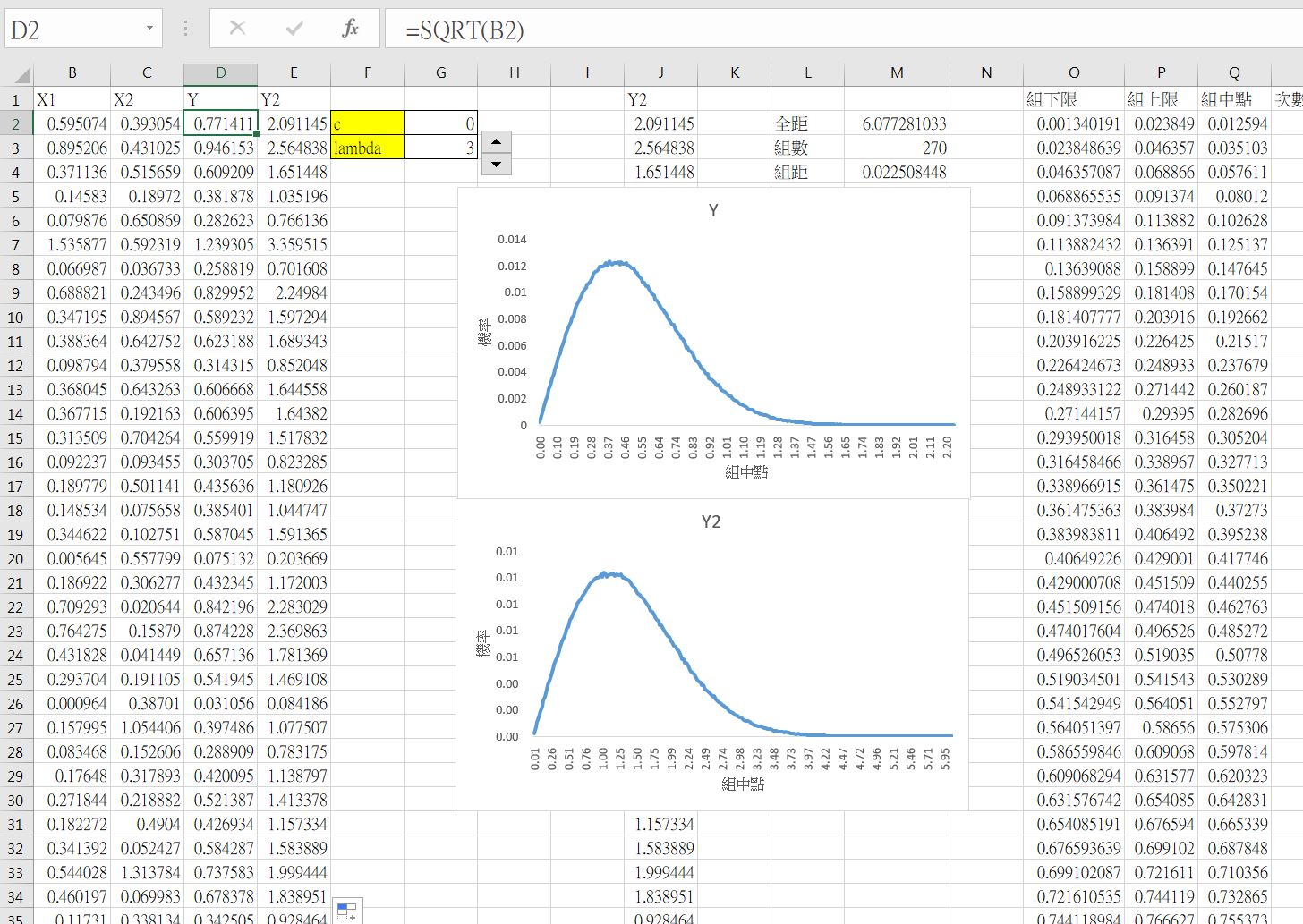
令$X$服從指數分配,參數為$\lambda$。
\[Y=\sqrt{X} \sim Rayleigh(\frac{1}{\sqrt{2\,\lambda}}) \\ f_{Y}(y)= \frac{2 \,y}{\sqrt{2\,\lambda}} \, e^{\frac{-y^{2}}{\sqrt{2\,\lambda}}}\]下圖中的 Y2 為直接使用雷利夫分配模擬數據。
5. 與logistic分配關係
假設兩獨立隨機變數,$X_{1}, X_{2}$,分別服從指數分配,參數為$\lambda = 1$。
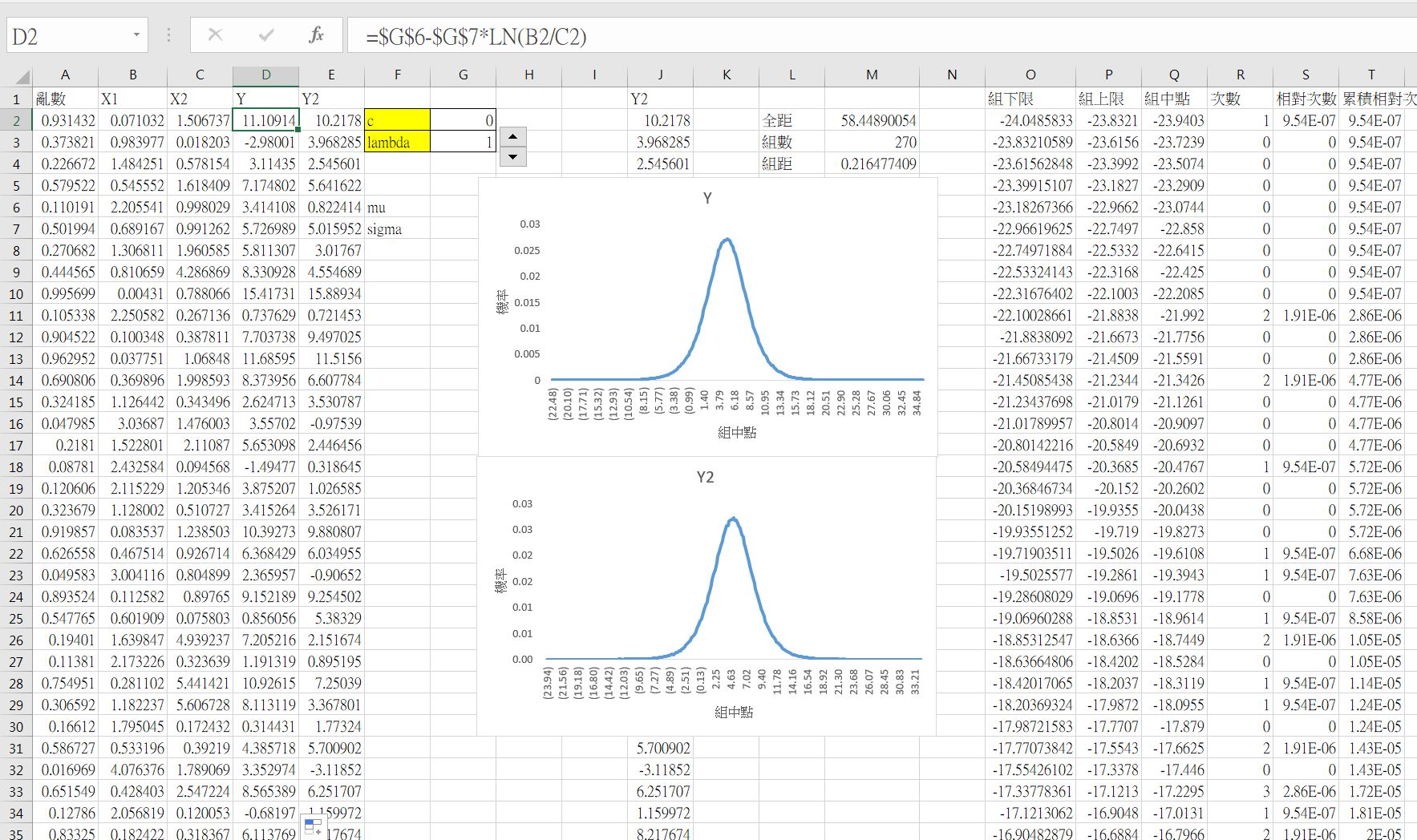
令logistic分配為 $Y_{2}$,參數為 $\mu$ 和 $\sigma$。在Excel操作中需要加入logsitic分配的參數,分列在 G6 和 G7 儲存格。
\[Y = \mu - \sigma \times ln(X_{1} / X_{2}) \sim logistic(\mu, \sigma)\]下圖中的 Y2 為直接使用logistic分配模擬數據。