美國消費者物價指數之所有城市消費者的消費者價格指數特性

發表於 | 分類於
字數統計 3053

1. 前言

美國在2022年6月10日公布5月的消費者通膨率於近12個月內達到8.6%，是40年來最高點(美國勞工部資料)。直接上美國聯準會(FED)的網站了解此這項消費者通貨膨脹率的計算基礎為「所有城市消費者的消費者價格指數：美國城市平均所有項」。

該數據在FED網站描述有

  • 基期：1982-1984=100
  • 數據頻率：月資料
  • 數據期間：1947年1月至2022年5月
  • 資料來源：美國勞工統計局
  • 代號：CPIAUCSL(已季節性調整)、CPIAUCNS(未經季節性調整)

本文主要使用CPIAUCSL數據，應用「機率分配模擬器」，了解美國消費者物價指數和通貨膨脹率告知我們哪些不為人知的秘密。

2. 數據說明

我接下來都使用CPIAUCSL數據，描述如下：

  • 經濟指標

    所有城市消費者的消費者價格指數：美國城市平均所有項目(CPIAUCSL)

    Consumer Price Index for All Urban Consumers: All Items in U.S. City Average

  • 特性

    「所有城市消費者的消費者價格指數：所有項目(CPIAUCSL)」是城市消費者支付的一籃子商品和服務的價格指數。

    1. 價格指數的百分比變化衡量任何兩個時間段之間的通貨膨脹率。最常見的通脹指標是一年前的百分比變化。
    2. 這也可以代表城市消費者的購買習慣。
    3. 這一特定指數包括美國大約88%的總人口，包括工薪階層、文員、技術工人、個體經營者、短期工人、失業者、退休人員和非勞動力。

  • 優勢1

    除了最初發布的未經調整的指數外，美國勞工統計局還發布了經季節性調整的指數。

    未經調整的系列反映了可能影響價格變化的所有因素。但是，觀察經季節性調整的CPI可能非常有用，因為它消除了季節性變化的影響，例如天氣。

  • 優勢2

    CPI 可用於識別通貨膨脹和通貨緊縮的時期。

    短期內 CPI 的顯著上升可能表明一段通貨膨脹，而短期內 CPI 的顯著下降可能表明一段通貨緊縮。

    由於CPI包括波動的食品和石油價格，它可能不是衡量通脹和通縮時期的可靠指標。為了更準確的檢測，通常使用核心CPI (CPILFESL)。

  • 限制

    1. 使用 CPI 時，請注意它並不適用於所有消費者，也不應用於確定相對生活成本。
    2. CPI 是一種容易受到抽樣誤差影響的統計量度，因為它是基於價格樣本而非完整平均值。

3. 消費者物價指數的基本描述

3.1. 直方圖

根據機率分配模擬器的Excel方法將所有的CPIAUCSL數據繪製出270組的直方圖，觀察下圖可發現，從1947年開始的CPIAUCSL數據多數集中在50以下。

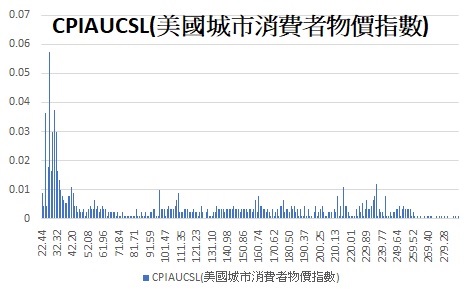
3.2. 敘述統計表

係數 數值
sample Mean 115.18666
Geometrical Mean 83.55901
Harmonic Mean 58.95508
sample variance 6631.61584
sample S.D. 81.43473
Skewed Coef. 0.38426
Kurtosis Coef. 1.70953
MAD 72.49172
Range 269.99400
MIN 21.48000
MAX 291.47400
Median 104.70000
Q1 31.75000
Q2 104.70000
Q3 183.70000
IQR 151.95000
C.V. 0.70698

3.3. 尋找機率模型

我將使用「改良式適合度檢定」和「曲線配適的隨機變數法」測定CPIAUCSL數據的機率模型。如果改良式適合度檢定可以測定出數據的機率模型，就不再使用第二種方法。

3.3.1. 改良式適合度檢定

由於我不知道CPIAUCSL數據為何種機率分配，所以就選擇完整的45種分配檢定。

45種分配檢定後，可得到最佳的分配為

H0: population distribution ~ Beta prime($\alpha = 95.897974, \beta = 1.609893$), H1: against H0

pearson goodness of fit

class [ 1 ] [ 2 ] [ 3 ] [ 4 ] [ 5 ] [ 6 ] [ 7 ] [ 8 ] [ 9 ] [ 10 ]
lower limit 8.86380 28.15771 37.44375 46.79033 57.27378 69.94769 86.26887 108.92708 144.39079 212.51437
upper limit 28.15771 37.44375 46.79033 57.27378 69.94769 86.26887 108.92708 144.39079 212.51437  
observed no 126.00000 148.00000 50.00000 31.00000 32.00000 20.00000 60.00000 91.00000 178.00000 169.00000
probability 0.10000 0.10000 0.10000 0.10000 0.10000 0.10000 0.10000 0.10000 0.10000 0.10000
expected no 90.50000 90.50000 90.50000 90.50000 90.50000 90.50000 90.50000 90.50000 90.50000 90.50000
chi square 13.92541 36.53315 18.12431 39.11878 37.81492 54.91989 10.27901 0.00276 84.59945 68.09116

degree of freedom=7

chi square test=363.408840

p value=0.000000

由於 P value值小於0.05，拒絕虛無假設。雖然已從45種機率分配的適合度檢定中得到最佳的Prime beta分配，但並未通過適合度檢定。

3.3.1. 曲線配適的隨機變數法

觀察數據的直方圖，決定切割為5部分，並且每部分估算最高30次方。每個部份的估算數學式如下圖。

由曲線配適得到的數學式就能夠開始模擬數值，此時模擬1百萬筆後，經過270組產生直方圖。

上圖可發現曲線配適得到的模擬值和實際數據的直方圖非常相近。

3.4. 建立數學模型

令Y=CPIAUCSL數據，視為應變數(dependent variable)，X=時間變數，為自變數(independent variable)，所以可得到數學式為

\[Y_{t} = H(X_{t})+\varepsilon_{t} \\ Y_{t} = H(X_{t}) \pm G(X_{t})+\delta_{t}\]

上式的 $H(\cdot)$ 為期望值模型，$G(\cdot)$ 為變異數異質性模型，$\varepsilon_{t}$ 和 $\delta_{t}$ 為誤差。此處變異數異質性模型中的應變數為 $\vert \hat{\varepsilon}_{t} \vert$。

一階自我相關誤差模型的應變數為 $u_{t}=\hat{\varepsilon}{t} / G(X{t})$，數學式為

\[u_{t} = \rho \, u_{t-1} + \phi_{t}\]

其中， $\rho$ 為自我相關係數(autocorrelation coefficient)，$\phi_{t}$ 為我們可以得到的最乾淨誤差。

上圖各欄分別為

  • 第一欄為期望值模型
    • 第一圖：CPIAUCSL原數據的走勢圖
    • 第二圖：CPIAUCSL的期望值估計圖
    • 第三圖：合併第一和第二圖
    • 第四圖：原數據和估計值的關係
  • 第二欄為變異數異質性模型
    • 第一圖：期望值模型得到的殘差，取絕對值後的走勢圖
    • 第二圖：變異數異質性的估計值
    • 第三圖：合併第一和第二圖
    • 第四圖：殘差絕對值和變異數異質性的估計值的關係
  • 第三欄為期望值模型 + 變異數異質性模型
    • 第一圖：CPIAUCSL的估計圖
    • 第二圖：原數據和估計值圖
    • 第三圖：原數據和估計值的關係
  • 第四欄為期望值模型 + 變異數異質性模型 + 一階自我相關誤差模型
    • 第一圖：CPIAUCSL的估計圖
    • 第二圖：原數據和估計值圖
    • 第三圖：原數據和估計值的關係

使用最佳化的模型方法可以看出變異數一直下降。而得到的 $\phi_{t}$可經由改良式適合度檢定得到柯西分配。

3.5. 變異數異質性模型的功用

我使用變異數異質性模型的高低點區隔出「所有城市消費者的消費者價格指數：所有項目(CPIAUCSL)」的波動下降區段，有：

  1. 1949年02月 ~ 1950年08月
    • 美國衰退期 1948年12月~1949年10月
  2. 1952年06月 ~ 1954年08月
    • 美國衰退期 1953年7月~1954年5月
  3. 1957年12月 ~ 1960年12月
    • 美國衰退期 1957年7月~1958年4月；1960年4月~1961年2月
  4. 1964年10月 ~ 1969年03月
  5. 1979年04月 ~ 1986年03月

    • 美國衰退期

      1969年12月~1970年12月；

      1973年11月~1975年4月；

      1979年12月~1980年7月；

      1981年7月~1982年11月

  6. 1991年03月 ~ 1996年07月
    • 美國衰退期 1990年7月~1991年3月
  7. 2001年07月 ~ 2004年07月
    • 美國衰退期 2001年3月~2001年11月
  8. 2009年02月 ~ 2013年01月
    • 美國衰退期 2007年12月~2009年6月
  9. 2015年08月 ~ 2017年12月
  10. 2019年12月 ~ 2020年11月
    • 美國衰退期 2020年2月~2020年4月
  11. 2021年11月 ~

這是根據CPIAUCSL原始數據估算出的變異數異質性模型切割出變異數異質性下降期間。這點是目前全球無法得到的數學模型，也是無法從過去的數據分析方法得到此特性！

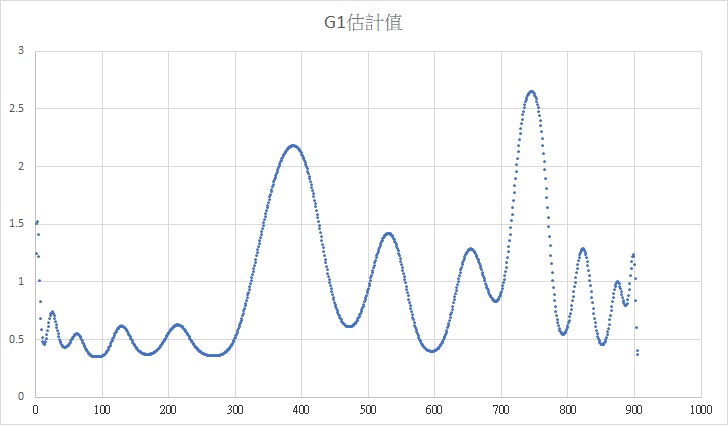
由上圖可切割出11個下降期間，對應上方的11點期間。我同時對應出美國聯準會認為的經濟衰退期。