前言

我在之前的部落格文中都以美國通貨膨脹率為討論目標。當時雖然是使用多線段法，由AI來反覆運算每新的一點加入後的趨勢線，以判定係數若下降則重新開始新的趨勢。而還有一個控制參數為每次新開始的趨勢需要設定「至少N筆數據量」。此參數同樣也能由AI來做運算和判斷。對此，MathGPT已經由AI判斷每條趨勢線的「判定係數」大小和「至少N筆數據量」。

有關MathGPT for numerical modelling軟體，請參考 Github。

接下來，讓我使用MathGPT for numerical modelling軟體為英國通貨膨脹率運算出最佳的趨勢數學模型吧。

資料來源

英國通貨膨脹率來自英國的Office for National Statistics。
指標名稱：Consumer price inflation time series (MM23)
網址：https://www.ons.gov.uk/economy/inflationandpriceindices/timeseries/l55o/mm23
數據期間：2016年1月到2023年3月
數據總量：85筆

方法

多線段的直線模式：由AI決定最佳的解釋力和每條趨勢線的最佳至少數據量
自變數 = X = 時間變數
應變數 = Y = 每月的英國通貨膨脹率

趨勢結果

當AI自行從英國通貨膨脹率中找出每條最佳趨勢線後，整體期間的解釋力達 $R2 = 0.994950$ 且均方差為 $MSE = 0.041111$。而AI找出的最佳至少數據量為 minimum number of each line = 5。

我們可以用每條趨勢線對應的數學方程式，計算出估計值，並繪製出英國通貨膨脹率的趨勢線(見下圖橘點)。但使用單一色的估計值並無法在圖形上顯現時間訊號，所以改以不同顏色表示每條趨勢線後，MathGPT告訴我們最新一條趨勢線從2022年6月到2023年1月，目前仍未見到有趨勢反轉。

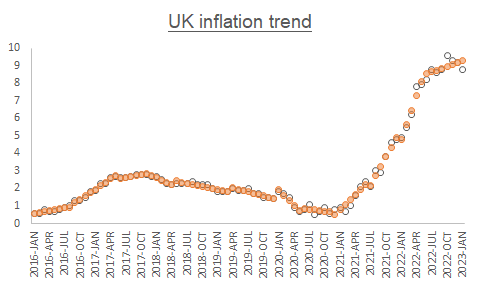
最新一條趨勢線持續8個月，並且估計方程式為 $Y = 0.083333 + 0.108333 X$，此趨勢線的判定係數為 $R2 = 0.365462$ 且均方差為 $MSE = 0.142639$。$X$為時間代號，從1到85。從估計方程式的斜率可知，在這8個月中，平均每月增加0.1%的通貨膨脹率。

殘差圖顯示多線段直線模式所得到的殘差隨著愈接近最近，殘差愈大。而對應在高通膨位置顯示通貨膨脹率和趨勢線的距離明顯愈來愈大，很可能已經要反轉。當然因為趨勢線需要至少5筆數據才能跑，而近4個月的通貨膨脹率持續下降，還未達到「至少數據量」的設定。我們可以等2023年2月的通貨膨脹率公告後，再測定數字的數學模式。

小結

MathGPT for numerical modelling軟體非常方便且實用地幫助想知道數字規律的人發現規律情況。英國通貨膨脹率期間對應央行的政策可知，2021年12月開始升息，後續2022年2月、3月、5月、6月、8月、9月、11月、12月，以及最新的2023年2月，升息結果造成即使判定係數很高的數學模式也難以抓住近期殘差的大幅波動範圍。

而英國通貨膨脹率在2022年10月達最高後，持續3個月下降。這可以說從2020年12月開始起漲的通貨膨脹率在放任1年後，需要用多次的升息政策累計效果，拉動通貨膨脹率趨勢由升轉降。

經濟體系的通貨膨脹率是恐怖的怪獸，易升難跌，恰好和股市相反，所以政府對國家境內的物價如若無法有效調節和實用的訊號立即了解物價指數和通貨膨脹率的變化，則如脫韁野馬，在高通膨時需要花費更多的代價將之壓下。

附註

想得到這篇部落格文的文件檔，請下載：點這