趨勢圖解布蘭特原油期貨價格

發表於 | 分類於
字數統計 5089
如何做到圖解趨勢？趨勢建立需要精準的數字建模，所以使用MathGPT for numerical modelling (lines combined method)軟體幫助使用者的數字能夠建立精準的數學模式。方法優勢來自多線段法的使用。多線段法源於傳統迴歸分析，但不同之處在於多線段法將迴歸線的樣本數內化決定，自然能為數字配適出最優解。為什麼要尋找原油價格的趨勢？原油在新冠疫情解除後，各國經濟重啟中扮演很重要的能源角色。當俄烏戰爭持續超過一年後，G7對俄羅斯出口原油價格做價格上限。對布蘭特原油期貨價的趨勢情況變化會如何？就讓我用 MathGPT for numerical modelling 軟體(一個能夠為數字跑出精準趨勢的數學建模AI軟體)跑出趨勢圖。

數據來源

Brent Crude Oil Last Day Financ (BZ=F) ：Yahoo! Finance

NY Mercantile - NY Mercantile Delayed Price. Currency in USD

https://finance.yahoo.com/quote/BZ%3DF

我另外也有與tradingview上的布蘭特原油期貨價格(MOEX BR1!)去做比對，發現兩者不同。以2023年3月20日的收盤紀錄來看，雅虎顯示收盤為73.79美元，tradingview顯示73.32美元。

數據說明

名稱 Brent Crude oil
代號 BZ=F
頻率 日資料
單位 數字
季節 沒有季節調整
期間 2022年3月21日到2023年3月17日
筆數 110

趨勢圖

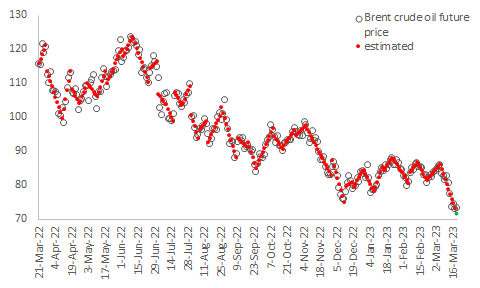
趨勢說明

  • 方法
    直線多線段法。每條趨勢線保持最佳解釋，每條直線函數配適得到解釋力，直到額外增加之數字導致解釋力下降，即重新新的趨勢線。

  • 每條趨勢線訊號

共38條趨勢線

line 1, 1.000000<=X<=5.000000, sorting order= 1 ~ 5, data number=5,

  • The estimated line Y=114.393000+1.361000*X,
  • R2=0.580204, MSE=4.467370, estimated sigma=2.113615,

line 2, 6.000000<=X<=14.000000, sorting order= 6 ~ 14, data number=9,

  • The estimated line Y=122.353333+-1.484667*X,
  • R2=0.837984, MSE=3.652870, estimated sigma=1.911248,

line 3, 15.000000<=X<=20.000000, sorting order= 15 ~ 20, data number=6,

  • The estimated line Y=58.740000+2.734286*X,
  • R2=0.827216, MSE=6.832057, estimated sigma=2.613820,

line 4, 21.000000<=X<=25.000000, sorting order= 21 ~ 25, data number=5,

  • The estimated line Y=129.293000+-1.001000*X,
  • R2=0.471934, MSE=3.737263, estimated sigma=1.933200,

line 5, 26.000000<=X<=30.000000, sorting order= 26 ~ 30, data number=5,

  • The estimated line Y=71.592000+1.276000*X,
  • R2=0.917603, SST=17.743800, SSR=16.281760, SSE=1.462040, MSE=0.487347, estimated sigma=0.698102,

line 6, 31.000000<=X<=36.000000, sorting order= 31 ~ 36, data number=6, The estimated line Y=130.446000+-0.676000*X, R2=0.105034, SST=76.137800, SSR=7.997080, SSE=68.140720, MSE=17.035180, estimated sigma=4.127370,

line 7, 37.000000<=X<=41.000000, sorting order= 37 ~ 41, data number=5, The estimated line Y=49.579000+1.563000*X, R2=0.690668, SST=35.371120, SSR=24.429690, SSE=10.941430, MSE=3.647143, estimated sigma=1.909750,

line 8, 42.000000<=X<=46.000000, sorting order= 42 ~ 46, data number=5, The estimated line Y=66.904000+1.028000*X, R2=0.812054, SST=13.013720, SSR=10.567840, SSE=2.445880, MSE=0.815293, estimated sigma=0.902936,

line 9, 47.000000<=X<=51.000000, sorting order= 47 ~ 51, data number=5, The estimated line Y=69.194000+0.996000*X, R2=0.222847, SST=44.515480, SSR=9.920160, SSE=34.595320, MSE=11.531773, estimated sigma=3.395846,

line 10, 52.000000<=X<=57.000000, sorting order= 52 ~ 57, data number=6, The estimated line Y=58.484381+1.141143*X, R2=0.881587, SST=25.849533, SSR=22.788623, SSE=3.060910, MSE=0.765228, estimated sigma=0.874773,

line 11, 58.000000<=X<=67.000000, sorting order= 58 ~ 67, data number=10, The estimated line Y=205.226485+-1.415576*X, R2=0.897419, SST=184.215010, SSR=165.318015, SSE=18.896995, MSE=2.362124, estimated sigma=1.536920,

line 12, 68.000000<=X<=72.000000, sorting order= 68 ~ 72, data number=5, The estimated line Y=83.602000+0.455000*X, R2=0.158943, SST=13.025080, SSR=2.070250, SSE=10.954830, MSE=3.651610, estimated sigma=1.910919,

line 13, 73.000000<=X<=77.000000, sorting order= 73 ~ 77, data number=5, The estimated line Y=160.402000+-0.734000*X, R2=0.075786, SST=71.089280, SSR=5.387560, SSE=65.701720, MSE=21.900573, estimated sigma=4.679805,

line 14, 78.000000<=X<=82.000000, sorting order= 78 ~ 82, data number=5, The estimated line Y=199.444000+-1.227000*X, R2=0.336301, SST=44.767320, SSR=15.055290, SSE=29.712030, MSE=9.904010, estimated sigma=3.147064,

line 15, 83.000000<=X<=87.000000, sorting order= 83 ~ 87, data number=5, The estimated line Y=187.375000+-0.963000*X, R2=0.661962, SST=14.009400, SSR=9.273690, SSE=4.735710, MSE=1.578570, estimated sigma=1.256412,

line 16, 88.000000<=X<=92.000000, sorting order= 88 ~ 92, data number=5, The estimated line Y=-5.476000+1.246000X, R2=0.823960, SST=18.842120, SSR=15.525160, SSE=3.316960, MSE=1.105653, estimated sigma=1.051501, line 17, 93.000000<=X<=97.000000, sorting order= 93 ~ 97, data number=5, The estimated line Y=255.358000+-1.664000X, R2=0.814494, SST=33.995280, SSR=27.688960, SSE=6.306320, MSE=2.102107, estimated sigma=1.449864, line 18, 98.000000<=X<=102.000000, sorting order= 98 ~ 102, data number=5, The estimated line Y=34.722000+0.629000X, R2=0.572838, SST=6.906680, SSR=3.956410, SSE=2.950270, MSE=0.983423, estimated sigma=0.991677, line 19, 103.000000<=X<=110.000000, sorting order= 103 ~ 110, data number=8, The estimated line Y=-18.657500+1.081667X, R2=0.773263, SST=63.549000, SSR=49.140117, SSE=14.408883, MSE=2.401481, estimated sigma=1.549671, line 20, 111.000000<=X<=120.000000, sorting order= 111 ~ 120, data number=10, The estimated line Y=282.516000+-1.617818X, R2=0.794411, SST=271.811760, SSR=215.930193, SSE=55.881567, MSE=6.985196, estimated sigma=2.642952, line 21, 121.000000<=X<=126.000000, sorting order= 121 ~ 126, data number=6, The estimated line Y=149.173810+-0.457143X, R2=0.398775, SST=9.170933, SSR=3.657143, SSE=5.513790, MSE=1.378448, estimated sigma=1.174073, line 22, 127.000000<=X<=132.000000, sorting order= 127 ~ 132, data number=6, The estimated line Y=283.029333+-1.499429X, R2=0.839953, SST=46.841933, SSR=39.345006, SSE=7.496928, MSE=1.874232, estimated sigma=1.369026, line 23, 133.000000<=X<=142.000000, sorting order= 133 ~ 142, data number=10, The estimated line Y=-73.790000+1.201818X, R2=0.876331, SST=135.976400, SSR=119.160273, SSE=16.816127, MSE=2.102016, estimated sigma=1.449833, line 24, 143.000000<=X<=148.000000, sorting order= 143 ~ 148, data number=6, The estimated line Y=203.552095+-0.763714X, R2=0.676156, SST=15.095683, SSR=10.207041, SSE=4.888642, MSE=1.222160, estimated sigma=1.105514, line 25, 149.000000<=X<=155.000000, sorting order= 149 ~ 155, data number=7, The estimated line Y=-16.185714+0.724643X, R2=0.826615, SST=17.787000, SSR=14.703004, SSE=3.083996, MSE=0.616799, estimated sigma=0.785366, line 26, 156.000000<=X<=162.000000, sorting order= 156 ~ 162, data number=7, The estimated line Y=16.865357+0.498214X, R2=0.454739, SST=15.283686, SSR=6.950089, SSE=8.333596, MSE=1.666719, estimated sigma=1.291015, line 27, 163.000000<=X<=177.000000, sorting order= 163 ~ 177, data number=15, The estimated line Y=252.441548+-0.957107X, R2=0.889126, SST=288.480133, SSR=256.495143, SSE=31.984990, MSE=2.460384, estimated sigma=1.568561, line 28, 178.000000<=X<=185.000000, sorting order= 178 ~ 185, data number=8, The estimated line Y=399.850000+-1.755833X, R2=0.907962, SST=142.609387, SSR=129.483929, SSE=13.125458, MSE=2.187576, estimated sigma=1.479046, line 29, 186.000000<=X<=190.000000, sorting order= 186 ~ 190, data number=5, The estimated line Y=30.880000+0.263000X, R2=0.050661, SST=13.653320, SSR=0.691690, SSE=12.961630, MSE=4.320543, estimated sigma=2.078592, line 30, 191.000000<=X<=196.000000, sorting order= 191 ~ 196, data number=6, The estimated line Y=-101.789143+0.949143X, R2=0.830870, SST=18.974400, SSR=15.765263, SSE=3.209137, MSE=0.802284, estimated sigma=0.895703, line 31, 197.000000<=X<=203.000000, sorting order= 197 ~ 203, data number=7, The estimated line Y=290.375714+-1.045714X, R2=0.579234, SST=52.860343, SSR=30.618514, SSE=22.241829, MSE=4.448366, estimated sigma=2.109115, line 32, 204.000000<=X<=208.000000, sorting order= 204 ~ 208, data number=5, The estimated line Y=-230.568000+1.519000X, R2=0.966956, SST=23.862120, SSR=23.073610, SSE=0.788510, MSE=0.262837, estimated sigma=0.512676, line 33, 209.000000<=X<=214.000000, sorting order= 209 ~ 214, data number=6, The estimated line Y=-71.290190+0.744571X, R2=0.849993, SST=11.413933, SSR=9.701766, SSE=1.712168, MSE=0.428042, estimated sigma=0.654249, line 34, 215.000000<=X<=224.000000, sorting order= 215 ~ 224, data number=10, The estimated line Y=254.303455+-0.775091X, R2=0.838013, SST=59.143690, SSR=49.563188, SSE=9.580502, MSE=1.197563, estimated sigma=1.094332, line 35, 225.000000<=X<=229.000000, sorting order= 225 ~ 229, data number=5, The estimated line Y=-76.822000+0.714000X, R2=0.826153, SST=6.170720, SSR=5.097960, SSE=1.072760, MSE=0.357587, estimated sigma=0.597986, line 36, 230.000000<=X<=235.000000, sorting order= 230 ~ 235, data number=6, The estimated line Y=309.848095+-0.972286X, R2=0.875199, SST=18.902483, SSR=16.543441, SSE=2.359042, MSE=0.589760, estimated sigma=0.767959, line 37, 236.000000<=X<=243.000000, sorting order= 236 ~ 243, data number=8, The estimated line Y=-54.071190+0.576905X, R2=0.931387, SST=15.008150, SSR=13.978402, SSE=1.029748, MSE=0.171625, estimated sigma=0.414276, line 38, 244.000000<=X<=252.000000, sorting order= 244 ~ 252, data number=9, The estimated line Y=435.543111+-1.438167*X, R2=0.878616, SST=141.244156, SSR=124.099402, SSE=17.144754, MSE=2.449251, estimated sigma=1.565008,

  • 整體估計結果
    • 時間序 1 ~ 37
    • R2 = 0.898837
    • MSE = 202.902886
    • 整體資料分割成7線,
    • 每條分割線樣本至少5資料個數

觀點

有意思的是，聯準會研究員Victoria Gregory和Elizabeth HardingFRED提出如何看出資訊產業的裁員水準是否增長太多，是以2022年4月為指數為100，其他數字全除以2022年4月的數字。用指數化後的數字來比較整體非農裁員水準和資訊產業裁員水準的比較。這種衡量方式可以看出資訊產業裁員人數是否在增加。如果是增加狀態，相對整體裁員人數還能看出是否增加過快。

我跟隨他們的部落格文，選擇資訊產業裁員水準的數據，建立趨勢模型，而不是跟著他們試圖用折線圖看出增長是否有過快跡象。特別是還得人為認定一個時間點為基準，將裁員人數做相除動作。他們認為這是一種數字標準化的動作，其中是否已經改變數字規律，就不得而知。