1. 概似函數的定義

概似函數為n個獨立隨機樣本的聯合機率，如下圖所示。概似函數是透過樣本了解母體分配參數對樣本的影響，並且找出反映母體參數的樣本數學組合為何。

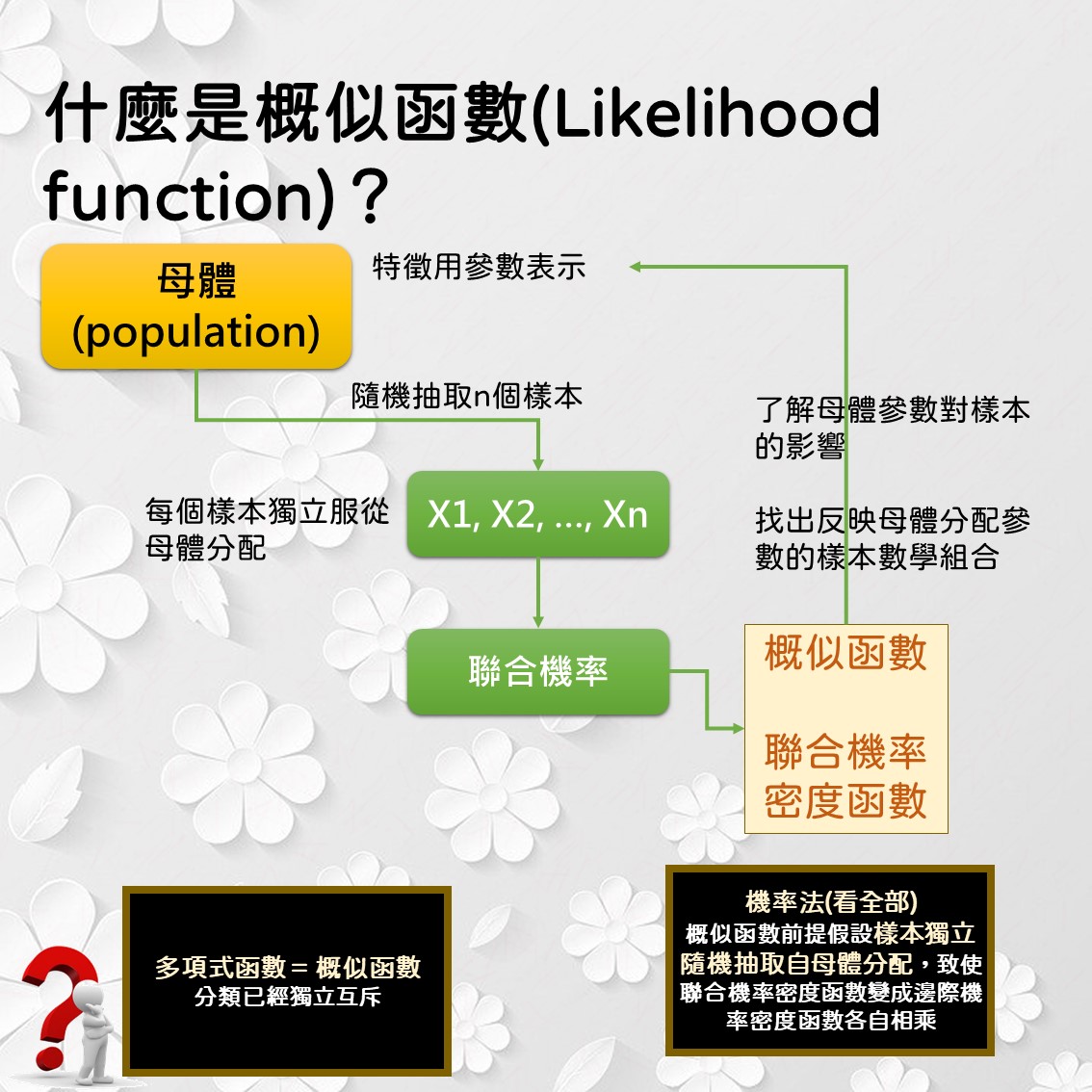
從定義中，我們可以歸納出2點：

從母體分配隨機獨立抽取n個樣本。很重要的是要獨立。這會讓聯合機率密度函數因獨立特性而直接相乘，無需考慮兩兩、三三、或更多的關聯。
n個獨立隨機樣本要建立聯合機率密度函數。這點影響很大。因為每個獨立隨機樣本來自母體，母體的機率密度函數就是某特定樣本的機率密度函數。

問題是我們取得樣本後，哪裡知道它的母體機率密度函數呢？如果知道母體機率函數，那麼就等同於母體機率分配已知，但未必知道母體參數之值。所以這點是最難的，也是特別耐人尋味。如上所述，你都知道樣本來自母體的機率密度函數，此時若變成母體參數已知，我們是使用機率了解樣本的變化了。若不知道母體參數，那我們就得使用統計去推估母體參數。

2. 概似函數能夠做什麼？

原本統計學是以樣本先取得後再去推估母體參數。母體的機率密度函數已知時，點估計量就能夠用概似函數獲得。使用概似函數得到點估計的方法稱為「最大概似法」，縮寫為MLE。

概似函數在微分前，需要將聯合機率密度函數轉成以是樣本為條件下的母體參數函數，亦即，

\[f \left(x_{1}, f_{2}, \cdots, x_{n}; \theta \right) = L \left(\theta \vert x_{1}, f_{2}, \cdots, x_{n} \right)\]

其中， $L(\bullet)$ 為最大概似法需要的概似函數形式。經過微分得到最大值所對應之樣本的數學組合後，此數學組合為母體參數的點估計量，稱為MLE估計量。

同樣是從母體隨機抽取n個樣本，使用以樣本為條件下，母體參數的概似函數找出母體參數的充分統計量。不過這個充分統計量和母體參數之間具有

\[E \left(U \vert 母體參數的點估計量(x) \right) = \phi(母體參數的點估計量)\]

$\phi(母體參數點估計量)$ 是母體參數的UMVUE。

概似函數是由獨立樣本的聯合機率為代表。聯合機率表示我們得先知道母體機率密度函數。然而當我們知道母體機率密度函數時，等於知道母體分配。但仍可推導出母體參數的點估計量。這相當於我們已知樣本服從的特定分配，但母體參數仍未知。