1. 前言

機率是統計之母。當我們知道機率模型或機率分配，就不需要再用統計了。然而當我們拿到數據後，並不知道數據的分配為何，這才需要使用統計方法了解母體參數。

機率和統計的關係就好比柏拉圖和亞里斯多德的哲學論點。他們的哲學理念皆是認為人們從既有的概念中賦予事物意義的認知。柏拉圖認為人類對所有事物的認知來自於一個理想的世界，在那的每個事物都是最完美的模型，永恆不變。人們一旦看到或聽到那個事物時就會自動產生事物的形象，並且是共通的形象。他認為現實世界中的所有事物都是理想世界產生的影子，短暫地出現在現實世界。

亞里斯多德則認為人類應該是先有現實世界的經驗感受後才有所有事物的概念認知，並且這個認知不是與生俱來的。他認為人類要先建構出對事物的經驗(或體驗)後才能定義出世界，所以人類必須努力去觀察大自然和各種人事物，收集到龐大的資料後，才能知道理想世界的每個人事物的原型。

現在，我們手邊的數據就如同亞里斯多德說的各種可觀察到的人事物或現象，而原型就是機率分配。統計就是不知道數據服從何種機率分配和母體參數未知下，我們得想辦法用這些數據去推定出母體參數為何。

不過，讓我強調一件事情：你也得先有原型概念。如果沒有原型概念，又怎麼會去比對呢？所以你有沒有發現柏拉圖或亞里斯多德的哲學論點的關鍵點呢？是的！總要能夠比對！

2. 我們得先知道母體

母體(population)指被調查對象的總集合。這是由研究人員自己設定的。調查對某事物的特性。母體的所有一切特性由事件、機率表示。但事件可能是分類形式，將之轉為數字表示時，事件對應到隨機變數。這些能夠對應到隨機變數的事件都是互斥事件。因此，母體特性會由隨機變數和對應之機率表示，稱為機率分配(probability distribuiton)。

機率分配由母體參數決定分配特性。常見的機率分配有很多，並且對應不同參數。

3. 我們得知道抽樣

統計的抽樣基於假設母體服從特定分配，這樣才能分析母體特性。我們會從母體中抽取出樣本。

樣本指母體的一部分資料，常用於推定母體參數或描述母體大概。

在樣本值還未被抽取出來前，皆被視為變動，為隨機變數，並且服從特定的母體機率分配。

另一個假設則是樣本之間為獨立的。除非是從有限的母體個數中抽取樣本，並且抽出不放回，造成樣本之間不獨立。

抽樣的方法有以下幾種：

簡單隨機抽樣
系統抽樣
分層抽樣
叢式抽樣

如果抽樣的個數=母體個數，稱為普查。

4. 樣本可以做什麼？

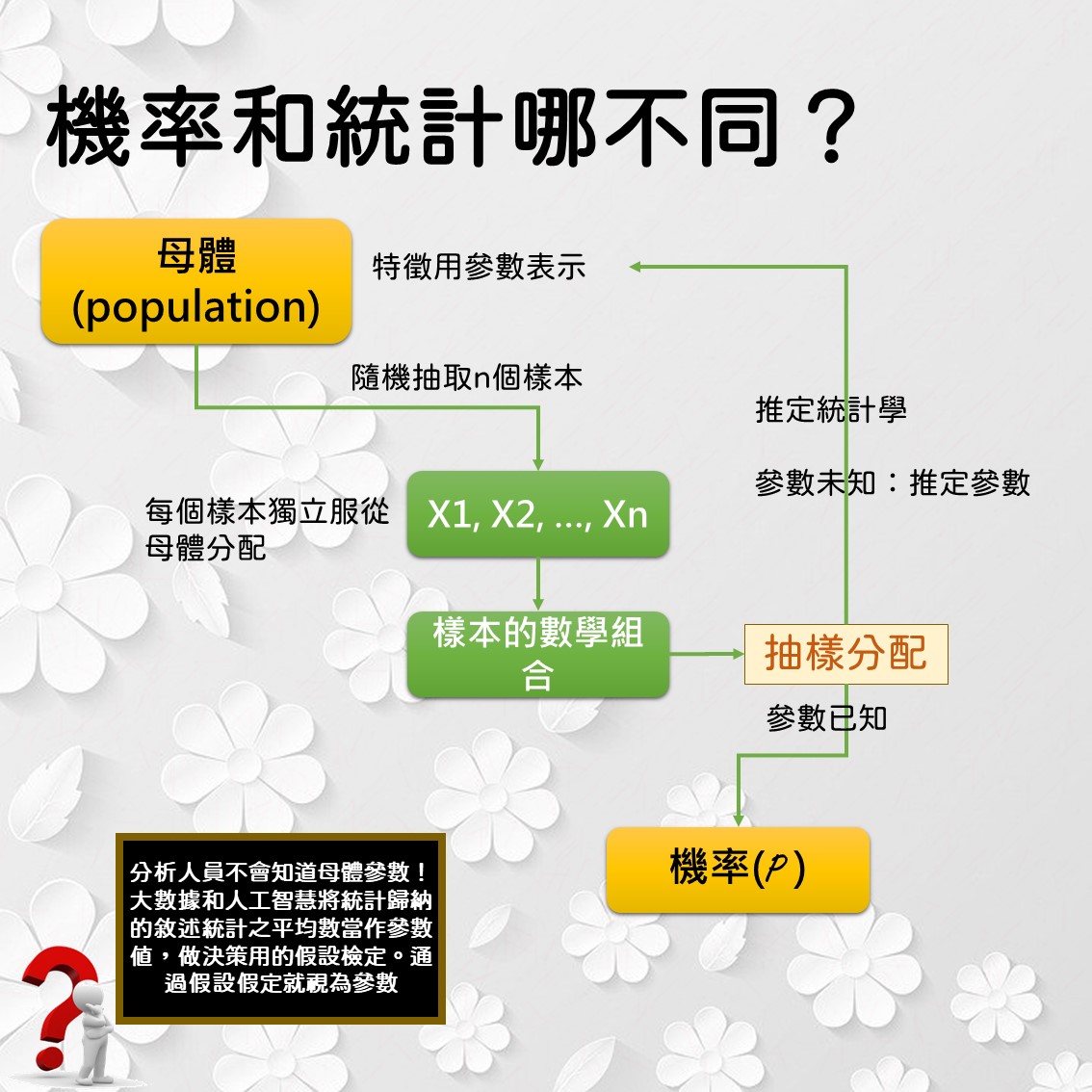
讓我們獲得一組樣本。如上圖所示，我們隨機獨立抽取出n個樣本，分別為$X_{1}, X_{2}, \cdots, X_{n}$。這裡使用的符號表示，代表樣本為變動，每個$X_{i}, i = 1, 2, \cdots, n$都是隨機變數。每個樣本服從特定母體機率分配，具有母體特性。

這些樣本可以計算敘述統計的係數，也可以繪製次數分配，另外還可以弄出各種的數學組合。你喜歡指數、對數、指數的指數或三角函數等都可以轉換出新的變數。新的變數稱為統計量(statistic)。常見的轉換是樣本加總、樣本平均、樣本變異數。

樣本的數學組合 = 統計量。統計量也是隨機變數。統計量也有分配，稱為抽樣分配(sampling distribution)。

5. 母體參數是否已經知道決定我們要做的是機率還是統計

到此我們還有一個事情沒有說，那就是你倒底知不知道母體參數？如果我們是在模擬數據，就會知道母體參數；而現實數據通常很難知道母體參數為何。

此處說「很難知道」不代表不知道。想知道現實數據如何知道母體機率分配和母體參數，參考我的3篇文章《如何找出一組數據的來源 - 一次45種機率分配》、《如何找出一組數據的來源 - 已知機率分配的適合度檢定》、《如何找出一組數據的來源 - 已知機率分配和分配參數》。

母體參數是否已知決定是用機率，還是統計。

如果母體參數已知，我們了解統計量的變化是機率。
如果母體參數未知，我們是用樣本得到的統計量去了解母體參數變化，這是統計。

這個差異可以用區間估計來說說。假設母體為常態分配，從中獨立隨機抽取n個樣本，建立統計量為樣本平均數，即

\[\overline{X}=\frac{X_{1}+X_{2}+ \cdots +X_{n}}{n} \sim N \left(\mu, \frac{\sigma^{2}}{n} \right)\]

將樣平均標準化為

\[\begin{equation} Z=\frac{\overline{X}-\mu}{\frac{\sigma}{\sqrt{n}}} \tag{1} \end{equation}\]

根據區間估計的概念得到

\[\begin{equation} P \left( \lvert Z \rvert \leq Z_{\frac{\alpha}{2}} \right) = 1 - \alpha \tag{2} \end{equation}\]

將(1)代入(2)，開展出兩條數學式分別為

\[\begin{equation} P \left(\mu - Z_{\frac{\alpha}{2}} \times \frac{\sigma}{\sqrt{n}} \leq \overline{X} \leq \mu + Z_{\frac{\alpha}{2}} \times \frac{\sigma}{\sqrt{n}} \right) = 1 - \alpha \tag{3} \end{equation}\]

和

\[\begin{equation} P \left(\overline{X} - Z_{\frac{\alpha}{2}} \times \frac{\sigma}{\sqrt{n}} \leq \mu \leq \overline{X} + Z_{\frac{\alpha}{2}} \times \frac{\sigma}{\sqrt{n}} \right) = 1 - \alpha \tag{4} \end{equation}\]

到這邊，我們得到(3)和(4)。你有沒有發現(3)和(4)的差異呢？是的！兩個不等式中間一個是樣本平均$\overline{X}$，一個是母體參數$\mu$。

對機率而言，因為母體參數皆為已知，所以我們是了解樣本平均的變化。對統計而言，因為母體參數未知，我們得利用樣本了解參數的變化。所以，式(3)為機率，式(4)為統計。

6. 小結

想了解機率和統計的不同，其實就在於母體參數是否已知。然而，我們在決定機率和統計不同之處前，還要先知道什麼是母體、母體機率分配、母體參數，還要知道什麼是樣本，怎樣抽樣，抽樣出來的樣本可以做什麼和產生什麼。如此我們才能夠去分辨要使用機率和是統計。