1. 前言
指數分配(Exponential distribution)是指數家族中第一個被學習者遇到分配,我們通常以符號 $X \sim \varepsilon(\lambda)$ 表示。
分配的圖形型態可以從Excel模擬得到,詳細如何使用Excel模擬指數分配,請參考【機率分配模擬器_prsimulated】粉絲專頁和公開社團。
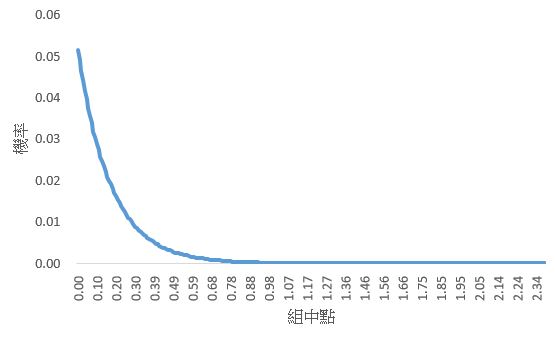
上圖使用1百萬筆數據,分為270組的分配直方圖。
2. 使用時機
我們何時會使用到指數分配呢?通常數據為衡量壽命(life time)、等候時間(Waiting time)等。所以參數 $\lambda$ 即反映單位時間內的某事件平均次數,例如一小時平均做五道題,代表 $\lambda = 5$ 題/小時。
3. 機率密度函數
指數分配的機率密度函數為
\[f_{X}(x)=\lambda \, e^{-\lambda \, x}, x \geq 0 \tag{1}\]式(1)的 $X$ 代表隨機變數,$\lambda$ 為參數,$\lambda = $ 平均次數 / 單位時間,$e$ 為自然指數。
我們可以令一個新的參數為 $\theta = 1 / \lambda$,代表平均時間/每次。此時,機率密度函數為
\[f_{X}(x)= \frac{1}{\theta} \, e^{-\frac{x}{\theta}}, x \geq 0 \tag{2}\]3.1. 機率和為1
根據隨機變數值的範圍對機率密度函數做積分,可得到整體面積為1。
\[\begin{matrix} \int_{0}^{\infty} f(x) dx &= \int_{0}^{\infty} \lambda \, e^{-\lambda \, x} dx \\ &= - e^{-\lambda \, x} \rvert_{0}^{\infty} \\ &= 1 \end{matrix} \tag{3}\]3.2. 動差母函數
\[\begin{align*} M_{X}(t) &= E(e^{t\,x}) = \int_{0}^{\infty} e^{t\,x} \, f(x) dx \\ &= \lambda \, \int_{0}^{\infty} e^{-(\lambda - t)\,x} \, dx = \frac{\lambda}{\lambda-t} \end{align*} \tag{4}\]其中, $\lambda -t > 0$。
式(4)可改寫為
\[\begin{align*} M_{X}(t) &= 1+\frac{t\,E(X)}{1!}+\frac{t^{2}\,E(X^{2})}{2!}+\frac{t^{3}\,E(X^{3})}{3!}+\cdots \\ &= 1+\frac{t}{\lambda}+\frac{t^{2}}{\lambda^{2}\times 2!}+\frac{t^{3}}{\lambda^{3}\times 3!}+\cdots \end{align*} \tag{5}\]根據式(5)得到 $E(X^{k})= k! / \lambda^{k}, k = 1, 2, 3, \cdots$。
動差母函數是計算各階動差的函數,所以我們可以得到一階動差(期望值)為
\[\left. E(X)=\frac{d\,M_{X}(t)}{dt} \right|_{t=0} = \left. \lambda\,(-1)\,(\lambda-t)^{-2}(-1) \right|_{t=0} \\ =\frac{1}{\lambda}\]二階動差為
\[\left. E(X^{2})=\frac{d}{dt}\frac{d\,M_{X}(t)}{dt} \right|_{t=0} = \left. \lambda\,(-2)\,(\lambda-t)^{-3}(-1) \right|_{t=0} \\ =\frac{2}{\lambda^{2}}\]從二階動差計算得到變異數為
\[Var(X) = E(X^{2})-\left[E(X)\right]^{2} \\ = \frac{2}{\lambda^{2}} - \left(\frac{1}{\lambda} \right)^{2} =\frac{1}{\lambda^{2}}\]從此處可得到指數分配的平均數和標準差值相等,亦即
\[\mu = \sigma = \frac{1}{\lambda}\]4. 特性
4.1. 無記憶
所謂無記憶特性是從機率的累加性來分辨的,定義為
\[P(X \geq t+s) = P(X \geq t)P(X \geq s)。\]舉例說明,如果 $P(X \geq 2)$,我們可以將t和s設定為 t = s = 1,所以,可得到
\[P(X \geq 1+1)=P(X \geq 1) \times P(X \geq 1)\]那如果是 $P(X \geq 3)$ 呢?此時可以得到
\(P(X \geq 2+1)=P(X \geq 2) \times P(X \geq 1)\) \(P(X \geq 3)=\big[P(X \geq 1) \big]^{3}\)
依此類推,就能得到無記憶特性的一般式為
\[P(X \geq x)=\big[P(X \geq 1) \big]^{x} \tag{6}\]累積機率分配的函數為 $F_{X}(x)=P(X \leq x)$
式(6)改寫為
\(1-F_{X}(x)=\big[P(X \geq 1) \big]^{x}\) \(1-\big(-e^{-\lambda x} +1 \big) =\big[P(X \geq 1) \big]^{x}\) \(e^{-\lambda x} =\big[P(X \geq 1) \big]^{x} \tag{7}\)
式(7)的等式右邊可改寫為
\[\big[P(X \geq 1) \big]^{x} = e^{x \, ln \big(P(X \geq x) \big)} \tag{8}\]根據式(7)和式(8),可得到
\[-\lambda =ln \big(P(X \geq x) \tag{9}\]那麼這樣的無記憶特性可以帶來怎樣的好處呢?這時候我們要計算條件機率變得簡單許多。因為
\[P(X \geq t+s) = P(X \geq t)P(X \geq s)\]條件機率為
\[P(X \geq t+s \vert X \geq t) = P(X \geq s)\]4.2. 右偏分配
根據三階動差可得到
\[E \bigg[\left(\frac{X-\mu}{\sigma}\right)^{3}\bigg]=\frac{E(X^{3})-3E(X^{2})\, \mu +2\,\mu^{3}}{1/\lambda^{3}}\\ =\frac{(6/\lambda^{3})-(6/\lambda^{3})+(2/\lambda^{2})}{1/\lambda^{3}} =2 > 0\]所以,偏態係數為正,代表分配為右偏分配。
4.3. 高峽峰
要確認分配是否為高峽峰或低闊峰的方式,得看峰態係數。而峰態係數源於四階動差。根據四階動差可得到
\[E \bigg[\left(\frac{X-\mu}{\sigma}\right)^{4}\bigg] = \frac{(3/\lambda^{4})+(6/\lambda^{4})+(1/\lambda^{4})}{1/\lambda^{4}} = 10\]所以可計算出峰態係數為 10 - 3 = 7
4.4. 眾數 = 0且為嚴格遞減函數
由圖形非常容易知道指數分配的眾數落在最左邊的$X$值。在指數分配沒有位移情況,原點即為眾數。
由機率密度函數可知道指數分配為嚴格遞減函數。
$X=0$的機率密度函數值為 $f(X=0)=\lambda \, e^{-\lambda \, 0} = \lambda$。
$X > 0$的機率密度函數為
- $f(X=1)=\lambda \, e^{-\lambda \, 1} = \lambda \, e^{-\lambda} < \lambda$。
- $f(X=2)=\lambda \, e^{-\lambda \, 2} = \lambda \, e^{-2\lambda} < \lambda \, e^{-\lambda}$。
4.5. 累積分配容易計算機率
只要計算機率時,就使用累積機率密度函數,$F(x) = 1 - e^{-\lambda \, x}$。
- $P(X \leq k) = F_{X}(k)$
- $P(X \geq k) = 1 - F_{X}(k)$
既然指數分配的累積機率很好使用,找中位數或四分位數都相對簡單。例如中位數為0.5機率對應的數值,
\[P(X < Median) = 0.5 = P(X > Median) \\ = 1 - F(Median) = e^{-\lambda \, Median} \\\]所以,中位數 = $ln(2) / \lambda$ 。
4.6. 失效率
失效率(Failure rate),又稱為故障率,是一個工程系統或零件失效的頻率。使用的計量單位為「單位通常會用每小時的失效次數」,符合指數分配參數的定義。所謂失效率是指工作到某一時間點仍未失效的產品,在過了該時間點後,單位時間內發生失效的機率。
令$t$代表時間點,當$X = t$, \(\lambda(t) = \frac{f(t)}{1-F(t)}=f(t \vert X \geq t) = \lambda\)
當 $X > t$,
\[f(x \vert X \geq t) = \frac{f \big(x \cap (X \geq t)\big)}{P(X \geq t)} = \frac{f(x)}{P(X \geq t)} = \lambda \, e^{-\lambda(x-t)}\]上式除了計算失效率外,還可成為指數分配位移的計算公式。例如,隨機變數X服從指數分配,參數為4,則位移到X大於等於5的機率密度函數為
\[f(x \vert X \geq 5) = 4\,e^{-4\,(x-5)}\]另一種位移方式來自「變數轉換」,此時我們得使用到微積分的Jacobian。
令$Y=X+t$,$X$服從指數分配,$x \geq 0$。我們要將$X$轉換成$Y$,所以先知道
- $\frac{dX}{dY}=1$
- $Y \geq t$
開始轉換,
\[f_{Y}(y)=f_{X}(y-t)=\lambda\,e^{-\lambda(y-t)}\vert \frac{dX}{dY}\vert = \lambda \, e^{-\lambda(y-t)}\]4.7. 參數值愈大,圖形愈陡峭
5. 和其他分配關係
5.1. 和Gamma分配
給定n個獨立隨機樣本,服從指數分配,樣本相加後,服從Gamma分配,參數為n和 $1/\lambda$。
5.2. 與常態分配關係
給定n個獨立隨機樣本,服從指數分配,
\[\frac{\overline{X}-\frac{1}{\lambda}}{\frac{1}{\lambda\,\sqrt{n}}} \xrightarrow[n\rightarrow \infty]{C.L.T.} N(0,1)\]5.3. 與均勻分配關係
假設兩獨立隨機變數,$X_{1}, X_{2}$,分別服從指數分配,參數為$\lambda$。
\[Y=\frac{X_{1}}{X_{1}+X_{2}} \sim U(0,1)\]這為分配的變數變換關係。
5.4. 與雙倍指數關係
假設兩獨立隨機變數,$X_{1}, X_{2}$,分別服從指數分配,參數為$\lambda$。
\[Y=X_{1}-X_{2} \sim Laplace(\lambda) \\ f_{Y}(y)=\frac{\lambda}{2} \, e^{-\lambda \vert y \vert}\]5.5. 與柏拉圖分配關係
- 假設兩獨立隨機變數,$X_{1}, X_{2}$,分別服從指數分配,參數為$\lambda$。
- 令$X$服從指數分配,參數為$\lambda$。
- 令$X$服從指數分配,參數為$\lambda$。
- 令$X$服從指數分配,參數為$\lambda$。
5.6. 與雷利夫分配關係
令$X$服從指數分配,參數為$\lambda$。
\[Y=\sqrt{X} \sim Rayleigh(\frac{1}{\sqrt{2\,\lambda}}) \\ f_{Y}(y)= \frac{2 \,y}{\sqrt{2\,\lambda}} \, e^{\frac{-y^{2}}{\sqrt{2\,\lambda}}}\]5.7. 取極小值還是指數
假設$n$個獨立隨機變數服從指數分配,各自的參數為$\lambda_{i}$。
$W=min \big(X_{1}, X_{2}, \cdots, X_{n} \big) \sim \varepsilon(\lambda_{1} + \lambda_{2} + \cdots + \lambda_{n})$